题目内容
5.计算:(1)23×(-5)-(-3)÷$\frac{3}{128}$;
(2)(-3)×$2\frac{2}{3}$+8×(-2$\frac{2}{3}$)-11÷(-$\frac{3}{8}$);
(3)(-1)2-(-1$\frac{3}{8}+2\frac{1}{3}-3\frac{3}{4}$)×(-24);
(4)$\frac{1}{2}×$(-2)2-($\frac{1}{3}$)3+[1+(-$\frac{2}{3}$)2×(-1$\frac{7}{8}$)].
分析 (1)原式先计算乘除运算,再计算加减运算即可得到结果;
(2)原式变形后,逆用乘法分配律计算即可得到结果;
(3)原式利用乘方的意义,以及乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-115+3×$\frac{128}{3}$=-115+128=13;
(2)原式=-3×$\frac{8}{3}$-8×$\frac{8}{3}$+11×$\frac{8}{3}$=$\frac{8}{3}$×(-3-8+11)=0;
(3)原式=1-33+56-90=57-123=-66;
(4)原式=$\frac{1}{2}$×4-$\frac{1}{27}$+1-$\frac{4}{9}$×$\frac{15}{8}$=2-$\frac{1}{27}$+1-$\frac{5}{6}$=3-$\frac{141}{162}$=2$\frac{21}{162}$=2$\frac{7}{54}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
12.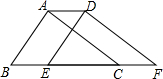 如图,将周长为8的△ABC沿BC方向平移n个单位得到△DEF,得四边形ABFD的周长为10,则n=( )
如图,将周长为8的△ABC沿BC方向平移n个单位得到△DEF,得四边形ABFD的周长为10,则n=( )
 如图,将周长为8的△ABC沿BC方向平移n个单位得到△DEF,得四边形ABFD的周长为10,则n=( )
如图,将周长为8的△ABC沿BC方向平移n个单位得到△DEF,得四边形ABFD的周长为10,则n=( )| A. | 2.5 | B. | 2 | C. | 1 | D. | 0.5 |
19.顺次连接一个矩形各边的中点,得到的四边形一定是( )
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
15. 如图,在?ABCD中,过点C作CE⊥AB,垂足为E,若∠BCE=42°,则∠D度数是( )
如图,在?ABCD中,过点C作CE⊥AB,垂足为E,若∠BCE=42°,则∠D度数是( )
 如图,在?ABCD中,过点C作CE⊥AB,垂足为E,若∠BCE=42°,则∠D度数是( )
如图,在?ABCD中,过点C作CE⊥AB,垂足为E,若∠BCE=42°,则∠D度数是( )| A. | 42° | B. | 48° | C. | 58° | D. | 138° |
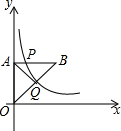 如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,
如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,