题目内容
6.已知AB∥CD.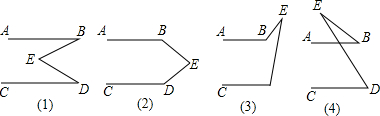
(1)如图(1),试问:∠B、∠D与∠E之间存在怎样的数量关系?
(2)如图(2),试问:∠B、∠D与∠E之间存在怎样的数量关系?
(3)如图(3),试问:∠B、∠D与∠E之间存在怎样的数量关系?
(4)如图(4),试问:∠B、∠D与∠E之间存在怎样的数量关系?
请写出你的结论,并从四个结论中选取一个进行证明.
分析 (1)过点E作EF∥AB,于是得到AB∥EF∥CD,根据平行线的性质即可得到结论;
(2)根据平行线的性质得到∠BEF=∠B,∠FED=∠D,根据角的和差即可得到结论;
(3)根据平行线的性质得到∠BEF=180°-∠B,∠FED=180°-∠D,于是得到∠DEB=∠BEF-∠FED=∠D-∠B;
(4)由平行线的性质得到∠BEF=180°-∠B,∠FED=180°-∠D,即可推出∠DEB=∠DEF-∠BEF=∠B-∠D.
解答 证明: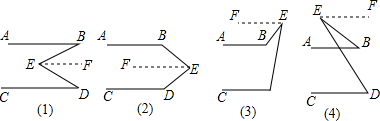 过点E作EF∥AB,
过点E作EF∥AB,
∴AB∥EF∥CD,
(1)如图(1),
∵∠BEF=∠B,∠FED=∠D,
∴∠B+∠D=∠BEF+∠FED,
即∠BED=∠B+∠D;
(2)∴∠BEF=∠B,∠FED=∠D,
∴∠B+∠D+∠BEF+∠FED=360°,
即∠BED+∠B+∠D=360°;
(3)∵∠BEF=180°-∠B,∠FED=180°-∠D,
∴∠DEB=∠BEF-∠FED=∠D-∠B;
(4)∵∠BEF=180°-∠B,∠FED=180°-∠D,
∴∠DEB=∠DEF-∠BEF=∠B-∠D.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
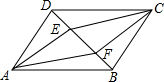 在?ABCD中,BD是对角线,AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AECF是平行四边形.
在?ABCD中,BD是对角线,AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AECF是平行四边形. 如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形.
如图,在?ABCD中,BE⊥AC于点E,DF⊥AC于点F,又M、N分别是DC、AB的中点,求证:四边形EMFN是平行四边形. 看图填理由:
看图填理由: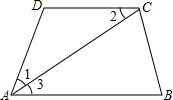 如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.
如图,AC平分∠DAB,∠1=∠2,试说明AB∥CD.