题目内容
11.甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工12天和乙队单独施工8天的工作量相同.(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了几天后,乙队因设备检修停止施工,剩下的工程由甲队单独完成,为及时完成工程,甲队将工作效率提高到原来的2倍,结果最终比原定完工时间多用了2天,则乙队一共施工了多少天?
分析 (1)设乙队单独完成此项任务需要x天,则甲队单独完成此项任务需要(x+10)天,根据甲队单独施工12天和乙队单独施工8天的工作量相同建立方程求出其解即可;
(2)设乙队一共施工了a天,根据甲、乙两队工作a天完成的工作量+甲队提高工作效率后($\frac{1}{\frac{1}{30}+\frac{1}{20}}$-a+2)天完成的工作量=1建立方程求出其解即可.
解答 解:(1)设乙队单独完成此项任务需要x天,则甲队单独完成此项任务需要(x+10)天,
由题意,得$\frac{12}{x+10}$=$\frac{8}{x}$,
解得:x=20.
经检验,x=20是原方程的解,
所以x+10=30.
答:甲队单独完成此项任务需要30天,乙队单独完成此项任务需要20天;
(2)设乙队一共施工了a天,由题意,得
($\frac{1}{30}$+$\frac{1}{20}$)a+2×$\frac{1}{30}$($\frac{1}{\frac{1}{30}+\frac{1}{20}}$-a+2)=1,
解得:a=4.
答:乙队一共施工了4天.
点评 本题是一道工程问题的应用题,考查了工作时间×工作效率=工作总量的运用,列分式方程与一元一次方程解实际问题的运用,解答分式方程时验根是学生容易忽略的地方.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | -x>-y | C. | x+3>y+2 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
16.一个正多边形中,每个外角等于它相邻内角的$\frac{2}{3}$,这个多边形的每个外角是( )
| A. | 15° | B. | 45° | C. | 36° | D. | 72° |
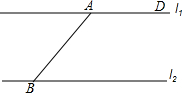 如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.