题目内容
16.一个正多边形中,每个外角等于它相邻内角的$\frac{2}{3}$,这个多边形的每个外角是( )| A. | 15° | B. | 45° | C. | 36° | D. | 72° |
分析 首先设多边形的内角为x°,则它的外角为$\frac{2}{3}$x°,根据多边形的内角与它相邻的外角互补可得方程x+$\frac{2}{3}$x=180,解方程可得内角的度数,进而得到外角的度数.
解答 解:设多边形的内角为x°,则它的外角为$\frac{2}{3}$x°,由题意得:
x+$\frac{2}{3}$x=180,
解得:x=108,
则它的外角是:180°-108°=72°,
故选:D.
点评 此题主要考查了多边形的内角和外角,关键是根据内角与相邻外角互补列出方程.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
4.某种型号的国产轿车行驶路程x(千米)和耗油y(升)可以表示为y=$\frac{2}{25}$x.
(1)根据上述关系式填写如表:
(2)分别写出这个问题中的自变量和因变量.
(1)根据上述关系式填写如表:
| 行驶路程x/千米 | 80 | 120 | 140 | 200 |
| 耗油量y/升 | $\frac{32}{5}$ | $\frac{48}{5}$ | $\frac{56}{5}$ | 16 |
 如图,直线AB,CD相交于O,OE⊥CD,OF⊥AB,∠DOF=65°,则∠BOE=65°,∠AOC=25°.
如图,直线AB,CD相交于O,OE⊥CD,OF⊥AB,∠DOF=65°,则∠BOE=65°,∠AOC=25°.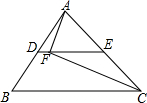 如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )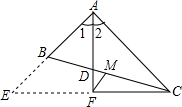 在△ABC中,AC>AB,M为BC的中点.AD是∠BAC的平分线,若CF⊥AD交AD的延长线于F.求证:MF=$\frac{1}{2}$﹙AC-AB﹚.
在△ABC中,AC>AB,M为BC的中点.AD是∠BAC的平分线,若CF⊥AD交AD的延长线于F.求证:MF=$\frac{1}{2}$﹙AC-AB﹚.