题目内容
12.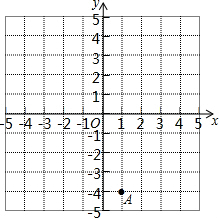 如图,在平面直角坐标系内,已知点A的位置;点B的坐标为(3,3);点C的坐标为(5,1).
如图,在平面直角坐标系内,已知点A的位置;点B的坐标为(3,3);点C的坐标为(5,1).(1)写出A的坐标,并画出△ABC;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)求四边形AB B1A1的面积.
分析 (1)根据A点在坐标系中的位置写出其坐标,由B、C的坐标找出两点,顺次连接各点即可;
(2)根据关于y轴对称的点的坐标特点画出△A1B1C1即可;
(3)根据梯形的面积公式即可得出结论.
解答  解:(1)由图可知,A(1,-4);
解:(1)由图可知,A(1,-4);
结论:所以△ABC即为所求作的三角形;
(2)所以△A1B1C1即为所求作的三角形;
(3)画出梯形的高AD,点A1、B1、D的坐标分别为
(-1,-4)、(-3,3)、(1,3)
因此S四边形ABB1A1=$\frac{1}{2}$×(2+6)×7=28.
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列从左到右的变形是因式分解的是( )
| A. | (x-4)(x+4)=x2-16 | B. | x2-y2+2=(x+y)(x-y)+2 | ||
| C. | x2+1=x(x+$\frac{1}{x}$) | D. | a2b+ab2=ab(a+b) |
7.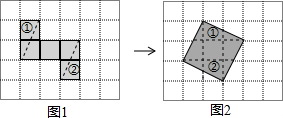 如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
 如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
17.如果a>b,那么下列结论中错误的是( )
| A. | a-1>b-1 | B. | 2a>2b | C. | $\frac{a}{3}$$>\frac{b}{3}$ | D. | -4a>-4b |
 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.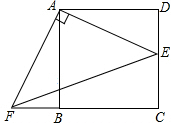 如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.
如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.