题目内容
2．先化简，再求值：$\frac{x+1}{1-x}$-$\frac{x+1}{{x}^{2}-1}$，其中x=2．分析 先根据分式混合运算的法则把原式进行化简，再把x=2代入进行计算即可．
解答 解：原式=$\frac{x+1}{1-x}$-$\frac{1}{x-1}$
=$\frac{x+1}{1-x}$+$\frac{1}{1-x}$
=$\frac{x+2}{1-x}$，
当x=2时，原式=$\frac{2+2}{1-2}$=-4．
点评 本题考查的是分式的化简求值熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
20．下列方程中，不是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}x+2y=0\\ 2x+y=1\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=0}\\{y-x+5=0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}x-2y-1=0\\-x=y+2\end{array}\right.$ | D． | $\left\{\begin{array}{l}x+y=4\\ 2x=z-2y\end{array}\right.$ |
13．下列计算，正确的是（ ）
| A． | （-$\sqrt{3}$）2=-3 | B． | $\sqrt{（-3）^{2}}$=-3 | C． | （2$\sqrt{6}$）2=24 | D． | $\sqrt{（π-3.2）^{2}}$=π-3.2 |
台风是一种自然灾害，它以台风中心为圆心在数十千米范围内形成气旋风暴，有极强的破坏力，据气象观察，距沿海某城市A正南256千米的B处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心正以15千米/时的速度沿北偏东30°方向向C移动，且台风中心风力不变，若城市受到的风力达到或超过四级，则称受台风影响．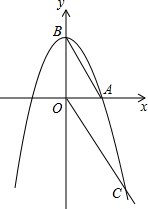
如图，抛物线y1=-x2+a与x轴正半轴交于点A，与y轴交于点B，点C（2，-3）在抛物线y1的图象上，连接AB，OC．
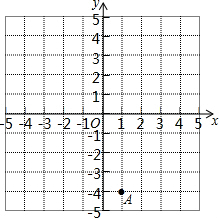如图，在平面直角坐标系内，已知点A的位置；点B的坐标为（3，3）；点C的坐标为（5，1）．