题目内容
5. 有这样一个问题:探究函数y=$\frac{2x-6}{x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{2x-6}{x-2}$的图象与性质.小慧根据学习函数的经验,对函数y=$\frac{2x-6}{x-2}$的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数y=$\frac{2x-6}{x-2}$的自变量x的取值范围是x≠2;
(2)列出y与x的几组对应值.请直接写出m的值,m=3;
| x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
| y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(4)结合函数的图象,写出该函数的两条性质:
①该函数图象是轴对称图形;②该函数图象不经过原点.
分析 (1)分式的分母不等于零;
(2)根据图表可知当y=0时所对应的x值为m,把y=0代入解析式即可求得;
(3)根据坐标系中的点,用平滑的直线连接即可;
(4)可以从对称性、增减性、渐近性、最值、连续性、与坐标轴交点、图象所在象限等方面作答.
解答 解:(1)依题意得:x-2≠0,
解得x≠2,
故答案是:x≠2;
(2)把y=0代入y=$\frac{2x-6}{x-2}$,得
0=$\frac{2m-6}{m-2}$,
解得m=3.
故答案是:3;
(3)如图所示: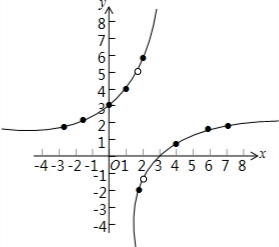
(4)由(3)中的图象得到:该函数图象是轴对称图形,该函数图象不经过原点等.
故答案是:该函数图象是轴对称图形,该函数图象不经过原点等.
点评 本题考查了反比例函数的图象和性质,根据图表画出函数的图象是解题的关键.

练习册系列答案
相关题目
13.下列各式中,从左到右的变形是因式分解的是( )
| A. | 4x2-1=(2x+1)(2x-1) | B. | a(x+y+1)=ax+ay+a | ||
| C. | (x+3y)(x-3y)=x2-9y2 | D. | a2c-a2b+1=a2(c-b)+1 |
10.一件产品原来每件的成本是100元,在市场售价不变的情况下,由于连续两次降低成本,现在利润每件增加了19元,则平均每次降低成本的( )
| A. | 8.5% | B. | 9% | C. | 9.5% | D. | 10% |
14. 已知二次函数y=$\frac{1}{2}{x^2}$.
已知二次函数y=$\frac{1}{2}{x^2}$.
(1)根据下表给出x的值,求出对应y的值后填写在表中;
(2)在给出的直角坐标系中画出函数y=$\frac{1}{2}{x^2}$的图象;
(3)根据图象指出,当x>0时,y随x的增大而增大还是减少?
 已知二次函数y=$\frac{1}{2}{x^2}$.
已知二次函数y=$\frac{1}{2}{x^2}$.(1)根据下表给出x的值,求出对应y的值后填写在表中;
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y=$\frac{1}{2}{x^2}$ | … | $\frac{1}{2}$ | $\frac{9}{2}$ | … |
(3)根据图象指出,当x>0时,y随x的增大而增大还是减少?
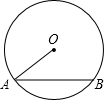 如图,⊙O的半径为6,OA与弦AB的夹角是30°,则弦AB的长度是6$\sqrt{3}$.
如图,⊙O的半径为6,OA与弦AB的夹角是30°,则弦AB的长度是6$\sqrt{3}$. 如图,OC是∠AOB的角平分线,∠BOD=$\frac{1}{3}$∠COD,∠BOD=20°,则∠AOD等于100°.
如图,OC是∠AOB的角平分线,∠BOD=$\frac{1}{3}$∠COD,∠BOD=20°,则∠AOD等于100°. 已知二次函数y=mx2+2(m+2)x+m+9.
已知二次函数y=mx2+2(m+2)x+m+9.