题目内容
20．
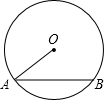如图，⊙O的半径为6，OA与弦AB的夹角是30°，则弦AB的长度是6$\sqrt{3}$．
分析 过O作OC⊥AB于C，根据垂径定理求出AB=2AC，根据含30°角的直角三角形性质求出OC，根据勾股定理求出AC，即可得出答案．
解答 解：过O作OC⊥AB于C，
∵OC过O，
∴AB=2AC，
∵OA=6，∠A=30°，
∴OC=$\frac{1}{2}$OA=3，由勾股定理得：AC=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$，
∵AB=2AC=6$\sqrt{3}$．
故答案为：6$\sqrt{3}$．
点评 本题考查了勾股定理，含30°角的直角三角形性质，垂径定理的应用，能根据垂径定理得出AB=2AC是解此题的关键．
练习册系列答案
相关题目
10．已知关于x的不等式组$\left\{\begin{array}{l}{x-a＞0}\\{5-2x＞1}\end{array}\right.$有且只有1个整数解，则a的取值范围是（ ）
| A． | a＞0 | B． | 0≤a＜1 | C． | 0＜a≤1 | D． | a≤1 |
11．下列给出的三条线段的长，其中能组成直角三角形的是（ ）
| A． | 62、82、102 | B． | 6、8、9 | C． | 2、$\sqrt{3}$、$\sqrt{5}$ | D． | $\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$ |
8．下列长度的三根木棒能组成三角形的是（ ）
| A． | 3，4，8 | B． | 4，4，8 | C． | 5，6，10 | D． | 6，7，14 |
5．
有这样一个问题：探究函数y=$\frac{2x-6}{x-2}$的图象与性质．
小慧根据学习函数的经验，对函数y=$\frac{2x-6}{x-2}$的图象与性质进行了探究．
下面是小慧的探究过程，请补充完成：
（1）函数y=$\frac{2x-6}{x-2}$的自变量x的取值范围是x≠2；
（2）列出y与x的几组对应值．请直接写出m的值，m=3；
（3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出该函数的两条性质：
①该函数图象是轴对称图形；②该函数图象不经过原点．
有这样一个问题：探究函数y=$\frac{2x-6}{x-2}$的图象与性质．小慧根据学习函数的经验，对函数y=$\frac{2x-6}{x-2}$的图象与性质进行了探究．
下面是小慧的探究过程，请补充完成：
（1）函数y=$\frac{2x-6}{x-2}$的自变量x的取值范围是x≠2；
（2）列出y与x的几组对应值．请直接写出m的值，m=3；
| x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
| y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
（4）结合函数的图象，写出该函数的两条性质：
①该函数图象是轴对称图形；②该函数图象不经过原点．
10．
如图，为了测得电视塔的高度AB，在D处用高为1米的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进120米达到F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（ ）
如图，为了测得电视塔的高度AB，在D处用高为1米的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进120米达到F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（ ）| A． | $60\sqrt{3}$ | B． | 61 | C． | $60\sqrt{3}+1$ | D． | 121 |