题目内容
15.计算$\sqrt{{9}^{2}+19}$;$\sqrt{9{9}^{2}+199}$;$\sqrt{99{9}^{2}+1999}$;$\sqrt{999{9}^{2}+19999}$的值,总结存在的规律,运用得到的规律可得:$\sqrt{\underset{\underbrace{99…9{9}^{2}}}{2016个}+\underset{\underbrace{199…99}}{2016个}}$=102016.(注:992=9801,9992=998001,99992=99980001,999992=9999800001)
分析 首先利用所给数据将各式化简,进而得出变化规律即可得出答案.
解答 解:∵$\sqrt{{9}^{2}+19}$=10;$\sqrt{9{9}^{2}+199}$=100=102;$\sqrt{99{9}^{2}+1999}$=1000=103;$\sqrt{999{9}^{2}+19999}$=10000=104,
∴$\sqrt{\underset{\underbrace{99…9{9}^{2}}}{2016个}+\underset{\underbrace{199…99}}{2016个}}$=102016.
故答案为:102016.
点评 此题主要考查了数字变化规律以及算术平方根,正确得出数据变化规律是解题关键.

练习册系列答案
相关题目
10.已知关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{5-2x>1}\end{array}\right.$有且只有1个整数解,则a的取值范围是( )
| A. | a>0 | B. | 0≤a<1 | C. | 0<a≤1 | D. | a≤1 |
5. 有这样一个问题:探究函数y=$\frac{2x-6}{x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{2x-6}{x-2}$的图象与性质.
小慧根据学习函数的经验,对函数y=$\frac{2x-6}{x-2}$的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数y=$\frac{2x-6}{x-2}$的自变量x的取值范围是x≠2;
(2)列出y与x的几组对应值.请直接写出m的值,m=3;
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
①该函数图象是轴对称图形;②该函数图象不经过原点.
 有这样一个问题:探究函数y=$\frac{2x-6}{x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{2x-6}{x-2}$的图象与性质.小慧根据学习函数的经验,对函数y=$\frac{2x-6}{x-2}$的图象与性质进行了探究.
下面是小慧的探究过程,请补充完成:
(1)函数y=$\frac{2x-6}{x-2}$的自变量x的取值范围是x≠2;
(2)列出y与x的几组对应值.请直接写出m的值,m=3;
| x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
| y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(4)结合函数的图象,写出该函数的两条性质:
①该函数图象是轴对称图形;②该函数图象不经过原点.
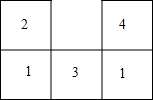 一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状如图所示.小正方形中的数字表示该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.
一个几何体由大小相同的小立方体搭成,从上面看到的几何体的形状如图所示.小正方形中的数字表示该位置的小立方块的个数.请你画出从正面和从左面看到的这个几何体的形状图.