题目内容
19.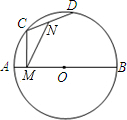 如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )| A. | 随C、D的运动位置而变化,且最大值为4 | |
| B. | 随C、D的运动位置而变化,且最小值为2 | |
| C. | 随C、D的运动位置长度保持不变,等于2 | |
| D. | 随C、D的运动位置而变化,没有最值 |
分析 连接OC、ON、OD,由垂径定理可知ON⊥CD,∠CON=∠DON,然后由∠ONC+∠CMO=180°,可证明O、N、C、M四点共圆,从而可得到∠NOC=∠NMC=30°,于是可证明△OCD为等边三角形,从而得到CD=2.
解答 解;连接:OC、ON、OD.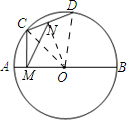
∵N是CD的中点,
∴ON⊥CD,∠CON=∠DON.
又∵CM⊥AB,
∴∠ONC+∠CMO=180°.
∴O、N、C、M四点共圆.
∴∠NOC=∠NMC=30°.
∴∠COD=60°.
又∵OC=OD,
∴△OCD为等边三角形.
∴CD=$\frac{1}{2}AB=\frac{1}{2}×4=2$.
故选:C.
点评 本题主要考查的是轨迹问题,发现O、N、C、M四点共圆,从而证得△OCD为等边三角形是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
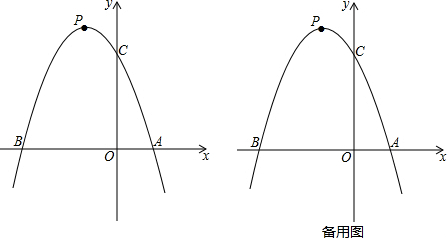
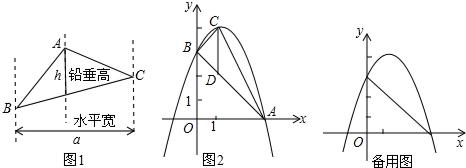
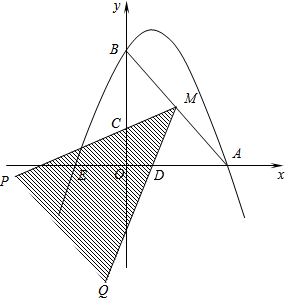 已知抛物线y=-$\frac{1}{2}$x2+bx+4与x轴和y轴的正半轴分别交于点A和B,已知B点坐标为(4,0).
已知抛物线y=-$\frac{1}{2}$x2+bx+4与x轴和y轴的正半轴分别交于点A和B,已知B点坐标为(4,0).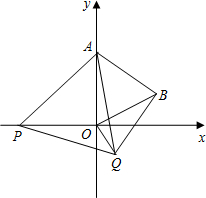 如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记点Q的位置为B,则当点P从(-2,0)运动到(2,0)时,点Q运动的路径长为4.
如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记点Q的位置为B,则当点P从(-2,0)运动到(2,0)时,点Q运动的路径长为4.