题目内容
9.解方程:(1)3x-4(2x+5)=x+4
(2)x-$\frac{x-1}{2}$=2-$\frac{x+2}{3}$
(3)$\frac{x-1}{0.3}$-$\frac{x+2}{0.5}$=12.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号得:3x-8x-20=x+4,
移项合并得:6x=-24,
解得:x=-4;
(2)去分母得:6x-3x+3=12-2x-4,
移项合并得:5x=5,
解得:x=1;
(3)方程整理得:$\frac{10x-10}{3}$-$\frac{10x+20}{5}$=12,即$\frac{10x-10}{3}$-2x-4=12,
去分母得:10x-10-6x-12=36,
移项合并得:4x=58,
解得:x=14.5.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
19.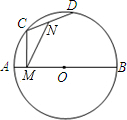 如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
 如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )| A. | 随C、D的运动位置而变化,且最大值为4 | |
| B. | 随C、D的运动位置而变化,且最小值为2 | |
| C. | 随C、D的运动位置长度保持不变,等于2 | |
| D. | 随C、D的运动位置而变化,没有最值 |
4.若单项式a4b-2m+1与-2a2mbn是同类项,则m+n的值为( )
| A. | 2 | B. | -2 | C. | -1 | D. | 1 |
14. 如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )
如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )
 如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )
如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 7cm |
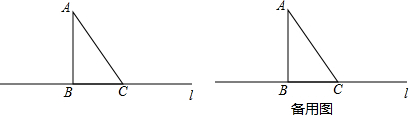
 如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,…第2015次输出的结果为3.
如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,…第2015次输出的结果为3.