题目内容
4.己知:a+$\frac{1}{a}$=1+$\sqrt{10}$,求a2+$\frac{1}{{a}^{2}}$、(a-$\frac{1}{a}$)2的值.分析 把a+$\frac{1}{a}$=1+$\sqrt{10}$两边平方,根据完全平方公式展开,即可解答.
解答 解:∵$a+\frac{1}{a}=1+\sqrt{10}$
∴$(a+\frac{1}{a})^{2}=(1+\sqrt{10})^{2}$,
${a}^{2}+2+\frac{1}{{a}^{2}}=1+2\sqrt{10}+10$,
${a}^{2}+\frac{1}{{a}^{2}}=9+2\sqrt{10}$,
$(a-\frac{1}{a})^{2}={a}^{2}-2+\frac{1}{{a}^{2}}=9+2\sqrt{10}-2$=7+2$\sqrt{10}$.
点评 本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.

练习册系列答案
相关题目
12.下列各组比例.满足Rt△ABC三边比的是( )
| A. | 1:2:3 | B. | 2:3:4 | C. | 3:4:5 | D. | 1:1:1 |
9.下列各式中,二次函数的个数是( )
①y=(2x-1)2-4x2+x;②y=-3x2+1;③y=ax2+bx+c;④y=2x2+$\frac{1}{x}$;⑤y=$\frac{{x}^{2}}{π}$+2x-1.
①y=(2x-1)2-4x2+x;②y=-3x2+1;③y=ax2+bx+c;④y=2x2+$\frac{1}{x}$;⑤y=$\frac{{x}^{2}}{π}$+2x-1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.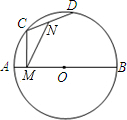 如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
 如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )
如图,AB为直径,AB=4,C、D为圆上两个动点,N为CD中点,CM⊥AB于M,当C、D在圆上运动时保持∠CMN=30°,则CD的长( )| A. | 随C、D的运动位置而变化,且最大值为4 | |
| B. | 随C、D的运动位置而变化,且最小值为2 | |
| C. | 随C、D的运动位置长度保持不变,等于2 | |
| D. | 随C、D的运动位置而变化,没有最值 |
 如图,AB=DE,AC=DF,BF=EC,△ABC和△DEF全等吗?请说明理由.
如图,AB=DE,AC=DF,BF=EC,△ABC和△DEF全等吗?请说明理由. 已知关于x的一元二次方程mx2-(m+1)x+1=0
已知关于x的一元二次方程mx2-(m+1)x+1=0