题目内容
13.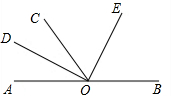 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.(1)图中∠BOD的邻补角为∠AOD,∠AOE的邻补角为∠BOE;
(2)如果∠COD=25°,那么∠BOE=65°,
如果∠COD=60°,那么∠BOE=30°;
(3)试猜想∠COD与∠BOE具有怎样的数量关系,并说明理由.
分析 (1)直接利用邻补角的定义分析得出答案;
(2)结合角平分线的定义利用已知分别得出各角度数即可;
(3)利用角平分线的定义结合平角的定义分析得出答案.
解答 解:(1)如图所示:∠BOD的邻补角为:∠AOD,
∠AOE的邻补角为:∠BOE;
故答案为:∠AOD,∠BOE;
(2)∵∠COD=25°,∴∠AOC=2×25°=50°,
∴∠BOC=130°,
∴∠BOE=$\frac{1}{2}$×130°=65°,
∵∠COD=60°,
∴∠AOC=120°,
∴∠BOC=60°,
∴∠BOE=$\frac{1}{2}$∠BOC=30°,
故答案为:65°,30°;
(3)由题意可得:
∠COD+∠BOE
=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC
=$\frac{1}{2}$(∠AOC+∠BOC)
=90°.
点评 此题主要考查了邻补角、角平分线的定义,正确把握定义是解题关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
18.若分式$\frac{1}{x+3}$的值大于0,则实数x的取值范围是( )
| A. | x>-3 | B. | x≥-3 | C. | x>3 | D. | x≠-3 |
2.列方程组解应用题:
在“某地大地震”灾民安置工作中,某企业捐助了一批板材24 000m2,某灾民安置点用该企业捐助的这批板材全部搭建成A,B两种型号的板房,供2 300名灾民临时居住.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
问:(1)该灾民安置点需搭建A型板房和B型板房各多少间?
(2)因对灾民人数估计不足,实际安置中A型板房超员15%,B型板房超员20%,则该安置点灾民实际有多少人?
在“某地大地震”灾民安置工作中,某企业捐助了一批板材24 000m2,某灾民安置点用该企业捐助的这批板材全部搭建成A,B两种型号的板房,供2 300名灾民临时居住.已知建一间A型板房和一间B型板房所需板材及能安置的人数如下表所示:
| 板房型号 | 所需板材 | 安置人数 |
| A型板房 | 54m2 | 5 |
| B型板房 | 78m2 | 8 |
(2)因对灾民人数估计不足,实际安置中A型板房超员15%,B型板房超员20%,则该安置点灾民实际有多少人?
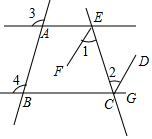 已知:如图,直线AE,BC被直线AB,EC所截,已知∠3=∠4,EF平分∠AEC,CD平分∠ECG,将下列证明EF∥CD的过程及理由填写完整.
已知:如图,直线AE,BC被直线AB,EC所截,已知∠3=∠4,EF平分∠AEC,CD平分∠ECG,将下列证明EF∥CD的过程及理由填写完整. 如图,在?ABCD中,E、F分别是AB、CD的中点,求证:四边形EBFD是平行四边形.
如图,在?ABCD中,E、F分别是AB、CD的中点,求证:四边形EBFD是平行四边形. 中的一个常数污染了.怎么办呢?小明想了一想,便翻看书后答案,此方程的解是y=-$\frac{5}{3}$,很快补好了这个常数,并迅速地完成了作业,同学们,你们能补出这个常数吗?它应是3.
中的一个常数污染了.怎么办呢?小明想了一想,便翻看书后答案,此方程的解是y=-$\frac{5}{3}$,很快补好了这个常数,并迅速地完成了作业,同学们,你们能补出这个常数吗?它应是3. 如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.