题目内容
13. 如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
如图,P为正方形ABCD 的边AD上的一动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.(1)证明:AE2+CF2=16.
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求此时DM的值.
分析 (1)根据垂直定义得出∠AEB=∠BFC=90°,AB=BC,结合∠ABE=∠BCF,证明△ABE≌△BCF,可得AE=BF,于是AE2+CF2=BF2+CF2=BC2;
(2)设AP=x,则PD=4-x,由已知∠DPM=∠PAE=∠ABP,△PDM∽△BAP,列出关于x的一元二次函数,求出DM的最大值.
解答 (1)证明:∵AE⊥BP,CF⊥BP,
∴∠AEB=∠BFC=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
又∵∠ABE+∠FBC=∠BCF+∠FBC,
∴∠ABE=∠BCF,
∵在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠AEB=∠BFC}\\{∠ABE=∠BCF}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCF(AAS),
∴AE=BF,
∴AE2+CF2=BF2+CF2=BC2=42=16;
(2)解:设AP=x,则PD=4-x,
∵四边形ABCD是正方形,
∴∠D=∠BAP=90°,∠DCB=90°,
∴∠DPM+∠DMP=90°,∠DCF+∠BCF=90°,
∵PM∥CF,
∴∠DMP=∠DCF,
∴∠DPM=∠BCF,
由(1)知:∠BCF=∠ABP,
∴∠DPM=∠ABP,
∵∠D=∠BAP,
∠DPM=∠PAE=∠ABP,
∴△PDM∽△BAP,
∴$\frac{DM}{AP}$=$\frac{PD}{BA}$,
即$\frac{DM}{4-x}$=$\frac{x}{4}$,
∴DM=$\frac{x(4-x)}{4}$=-$\frac{1}{4}$x2+x,
当x=2时,即点P是AD的中点时,DM有最大值为1.
点评 本题主要考查正方形的性质等知识点,解答本题的关键是熟练掌握全等三角形的判定定理以及三角形相似等知识,此题有一定的难度,是一道不错的中考试题.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案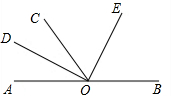 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC. 如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.
如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.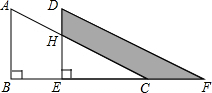 如图,直角△ABC沿点B到点C的方向平移到△DEF的位置,若AB=5,DH=1,平移距离为2,则阴影部分DHCF的面积等于4.
如图,直角△ABC沿点B到点C的方向平移到△DEF的位置,若AB=5,DH=1,平移距离为2,则阴影部分DHCF的面积等于4.