题目内容
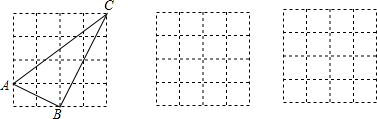
16. 如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米.
如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米.
分析 首先构造直角三角形,根据树高可得AB的长,然后再利用勾股定理计算出AC长即可.
解答  解:如图:
解:如图:
∵一棵高11米,另一棵高6米,
∴AB=11-6=5(米),
∵两树相距12米,
∴BC=12米,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13(米),
故答案为:13.
点评 此题主要考查了勾股定理得应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
 如图,已知△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F,且CF=3.求BF.
如图,已知△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F,且CF=3.求BF. 六一儿童节期间,某眼镜店开展优惠配镜活动,某款式的眼镜广告如图:请你为广告补上原价.
六一儿童节期间,某眼镜店开展优惠配镜活动,某款式的眼镜广告如图:请你为广告补上原价.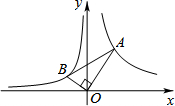 如图,已知第一象限内的点A在反比例函y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{2}$,则k的值为-1.
如图,已知第一象限内的点A在反比例函y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{2}$,则k的值为-1.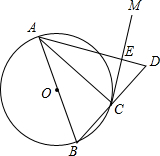 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.