题目内容
1.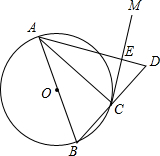 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求AC的长.
分析 (1)连接OC,由∠ABC+∠BAC=90°及CM是⊙O的切线得出∠ACM+∠ACO=90°,再利用∠BAC=∠ACO,得出结论,
(2)连接OC,得出△AEC是直角三角形,△AEC的外接圆的直径是AC,利用△ABC∽△CDE,求出AC.
解答 (1)证明:如图,连接OC,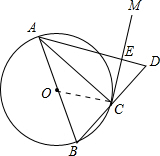
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
又∵CM是⊙O的切线,
∴OC⊥CM,
∴∠ACM+∠ACO=90°,
∵CO=AO,
∴∠BAC=∠ACO,
∴∠ACM=∠ABC;
(2)解:∵BC=CD,∠ACB=90°,
∴∠OAC=∠CAD,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠CAD,
∴OC∥AD,
又∵OC⊥CE,
∴AD⊥CE,
∴△AEC是直角三角形,
∴△AEC的外接圆的直径是AC,
又∵∠ABC+∠BAC=90°,∠ACM+∠ECD=90°,
∴△ABC∽△CDE,
∴$\frac{AB}{CD}$=$\frac{BC}{ED}$,
⊙O的半径为3,
∴AB=6,
∴$\frac{6}{CD}$=$\frac{BC}{2}$,
∴BC2=12,
∴BC=2$\sqrt{3}$,
∴AC=$\sqrt{36-12}$=2$\sqrt{6}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理、圆周角定理和相似三角形的判定与性质.解题的关键是找准角的关系.

练习册系列答案
相关题目
12.已知:⊙O1和⊙O2的直径分别为5cm和3cm,两圆的圆心距是9cm,则两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
13.0.02380的有效数字有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:OB=OE.
如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:OB=OE.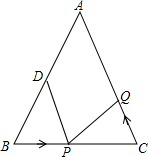 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动. 如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米.
如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米. 如图,圆锥的底面半径OB为10厘米,高AO为24厘米,它的侧面展开图扇形面积为260π厘米2.
如图,圆锥的底面半径OB为10厘米,高AO为24厘米,它的侧面展开图扇形面积为260π厘米2.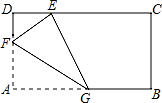 已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.如果折痕FG分别与AD、AB交于点F、G,AF=$\frac{2}{3}$,求五边形DFGBC的周长.
已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.如果折痕FG分别与AD、AB交于点F、G,AF=$\frac{2}{3}$,求五边形DFGBC的周长. 如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则:
如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则: