题目内容
5.如图,由若干个大小相同的小正方形组成的网格中.小华按下列要求作图:①顶点都在格点上的直角三角形;
②所画三角形的三边长度至少有两边长度是无理数.
小华在左边的网格中已经作出Rt△ABC,请你按照同样的要求,在右边的两个网格中各画一个直角三角形,并使三个网格中的直角三角形互不全等.
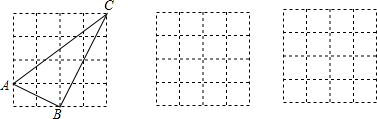
分析 在图1中,∠ABC=90°,由勾股定理得出AB=BC=2$\sqrt{2}$,即可画出图形;
在图2中,∠ABC=90°,由勾股定理得出AB=2$\sqrt{2}$,BC=$\sqrt{2}$,AC=$\sqrt{10}$,即可画出图形.
解答 解:作图如图1、图2所示: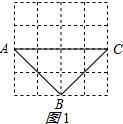
在图1中,由勾股定理得:
AB=BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,AC=4,
∵AB2+BC2=AC2,
∴∠ABC=90°;
在图2中,由勾股定理得:
AB=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,AC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,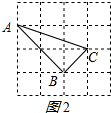
∵AB2+BC2=AC2,
∴∠ABC=90°.
点评 本题考查了正方形的性质、勾股定理、勾股定理的逆定理;熟练掌握勾股定理和勾股定理的逆定理,并能进行推理计算与作图是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.为了解滨江学校八年级学生的体重情况,从八年级8个班中每班随机抽取5名学生进行体重测试.在这个问题中,下列说法错误的是( )
| A. | 每个学生的体重是个体 | |
| B. | 40名学生的体重是一个样本 | |
| C. | 样本容量是5 | |
| D. | 全校八年级学生的体重的全体是总体 |
13.0.02380的有效数字有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20. 如图,过反比例函数y=$\frac{3}{x}$(x>0)图象上任意两点A、B分别作x轴的垂线,垂足为C、D,连接OA、OB.设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,则( )
如图,过反比例函数y=$\frac{3}{x}$(x>0)图象上任意两点A、B分别作x轴的垂线,垂足为C、D,连接OA、OB.设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,则( )
 如图,过反比例函数y=$\frac{3}{x}$(x>0)图象上任意两点A、B分别作x轴的垂线,垂足为C、D,连接OA、OB.设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,则( )
如图,过反比例函数y=$\frac{3}{x}$(x>0)图象上任意两点A、B分别作x轴的垂线,垂足为C、D,连接OA、OB.设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,则( )| A. | S1>S2 | B. | S1=S2 | ||
| C. | S1<S2 | D. | S1、S2的大小关系不确定 |
17. 为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
请结合图标完成下列问题:
(1)表中的a=14;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第2组;
(4)请简单谈谈你对这次测试结果的看法这次测试中成绩差的学生较多,需要多练习.
 为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:| 组别 | 次数 | 频数/人数 |
| 第1组 | 80≤x<100 | 21 |
| 第2组 | 100≤x<120 | 15 |
| 第3组 | 120≤x<140 | a |
| 第4组 | 140≤x<160 | 10 |
| 第5组 | 160≤x<180 | 9 |
(1)表中的a=14;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第2组;
(4)请简单谈谈你对这次测试结果的看法这次测试中成绩差的学生较多,需要多练习.
14.某公司10名职工3月份工资统计如下,该公司10名职工3月份工资的中位数是( )
| 工资(元) | 3000 | 3200 | 3400 | 3600 |
| 人数(人) | 3 | 3 | 3 | 1 |
| A. | 3100元 | B. | 3200元 | C. | 3300元 | D. | 3400元 |
 如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米.
如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米.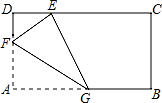 已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.如果折痕FG分别与AD、AB交于点F、G,AF=$\frac{2}{3}$,求五边形DFGBC的周长.
已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.如果折痕FG分别与AD、AB交于点F、G,AF=$\frac{2}{3}$,求五边形DFGBC的周长.