题目内容
6.在平面直角坐标系中有点A(1,2),B(3,4),在x轴上找一个P使P到A,B两点之间的距离和最小,则P点坐标为($\frac{5}{3}$,0).分析 A关于x轴的对称点A,求得A′B的函数解析式,然后求得解析式与x轴的交点即可.
解答 解:A关于x轴的对称点A′是(1,-2),
则设A′B的函数解析式是y=kx+b,
则$\left\{\begin{array}{l}{k+b=-2}\\{3k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=3}\\{b=-5}\end{array}\right.$,
则函数的解析式是y=3x-5.
当y=0时,3x-5=0,
解得:x=$\frac{5}{3}$,
则P的坐标是($\frac{5}{3}$,0).
故答案是($\frac{5}{3}$,0).
点评 本题考查了函数的对称,正确理解P就是直线A′B与x轴的交点是关键.

练习册系列答案
相关题目
17. 为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
请结合图标完成下列问题:
(1)表中的a=14;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第2组;
(4)请简单谈谈你对这次测试结果的看法这次测试中成绩差的学生较多,需要多练习.
 为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
为了进一步了解初中生的身体素质情况,体育老师对我校C161班69位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:| 组别 | 次数 | 频数/人数 |
| 第1组 | 80≤x<100 | 21 |
| 第2组 | 100≤x<120 | 15 |
| 第3组 | 120≤x<140 | a |
| 第4组 | 140≤x<160 | 10 |
| 第5组 | 160≤x<180 | 9 |
(1)表中的a=14;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第2组;
(4)请简单谈谈你对这次测试结果的看法这次测试中成绩差的学生较多,需要多练习.
14.某公司10名职工3月份工资统计如下,该公司10名职工3月份工资的中位数是( )
| 工资(元) | 3000 | 3200 | 3400 | 3600 |
| 人数(人) | 3 | 3 | 3 | 1 |
| A. | 3100元 | B. | 3200元 | C. | 3300元 | D. | 3400元 |
1.已知方程x2+x-3=0,则下列说法中,正确的是( )
| A. | 方程两根之和是1 | B. | 方程两根之积是3 | ||
| C. | 方程两根之平方和是7 | D. | 方程两根倒数之和是3 |
 如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米.
如图,有两棵树,一棵高11米,另一棵高6米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行13米.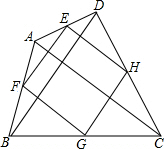 如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则:
如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则: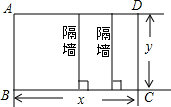 某工厂拟建一座平面图形是矩形且面积为200m2的三级污水处理池(如图所示),由于受地形限制,污水处理池的长与宽都不得超过16m,设污水处理池的一边长为xm,另一边长为ym.
某工厂拟建一座平面图形是矩形且面积为200m2的三级污水处理池(如图所示),由于受地形限制,污水处理池的长与宽都不得超过16m,设污水处理池的一边长为xm,另一边长为ym. 如图,在四边形ABCD中,AD∥BC,∠B=∠C,求证:AB=CD.
如图,在四边形ABCD中,AD∥BC,∠B=∠C,求证:AB=CD.