题目内容
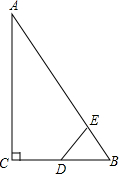 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,求t的值.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点.若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,求t的值.考点:相似三角形的判定与性质
专题:动点型,分类讨论
分析:先求出AB的长,再分①∠BDE=90°时,DE是△ABC的中位线,然后求出AE的长度,再分点E在AB上和在BA上两种情况列出方程求解即可;②∠BED=90°时,利用∠B的余弦列式求出BE,然后分点E在AB上和在BA上两种情况列出方程求解即可.
解答:解:∵∠ACB=90°,∠ABC=60°,BC=2cm,
∴AB=BC÷cos60°=2÷
=4,
①∠BDE=90°时,
∵D为BC的中点,
∴DE是△ABC的中位线,
∴AE=
AB=
×4=2(cm),
点E在AB上时,t=2÷1=2(秒),
点E在BA上时,点E运动的路程为4×2-2=6(cm),
∴t=6÷1=6(秒)(舍去);
②∠BED=90°时,BE=BD•cos60°=
×2×
=0.5,
点E在AB上时,t=(4-0.5)÷1=3.5(秒),
点E在BA上时,点E运动的路程为4+0.5=4.5(cm),
t=4.5÷1=4.5(秒),
综上所述,t的值为2或3.5或4.5.
∴AB=BC÷cos60°=2÷
| 1 |
| 2 |
①∠BDE=90°时,
∵D为BC的中点,
∴DE是△ABC的中位线,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
点E在AB上时,t=2÷1=2(秒),
点E在BA上时,点E运动的路程为4×2-2=6(cm),
∴t=6÷1=6(秒)(舍去);
②∠BED=90°时,BE=BD•cos60°=
| 1 |
| 2 |
| 1 |
| 2 |
点E在AB上时,t=(4-0.5)÷1=3.5(秒),
点E在BA上时,点E运动的路程为4+0.5=4.5(cm),
t=4.5÷1=4.5(秒),
综上所述,t的值为2或3.5或4.5.
点评:本题考查了三角形的中位线定理,解直角三角形的相关知识,难点在于分情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
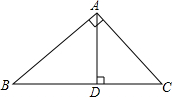 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则| AD |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
三条互不重合的直线的交点个数可能是( )
| A、0,1,3 |
| B、0,2,3 |
| C、0,1,2,3 |
| D、0,1,2 |
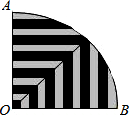 将如图所示的圆心角为90°的扇形条纹纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),OA=OB=8,则围成的圆锥形纸帽的高是
将如图所示的圆心角为90°的扇形条纹纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),OA=OB=8,则围成的圆锥形纸帽的高是 如图,数轴上线段AB的中点表示的数是
如图,数轴上线段AB的中点表示的数是 如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°-
如图,已知BO,CO分别是∠ABC的外角平分线,试说明∠BOC=90°-