题目内容
某市20名下岗职工在郊区承包50亩土地办农场,要求在这块土地上种蔬菜,烟叶和小麦.已知:一名职工可以中蔬菜2亩或烟叶3亩或小麦4亩,且每亩蔬菜可获利1100元,每亩烟叶可获利750元,每亩小麦可获利600元,若要求每亩地都要种上农作物,每种农作物都种,且20名职工都有工作,
(1)有哪几种种植方案?
(2)通过计算,请指出哪种种植方案获利最高?
(1)有哪几种种植方案?
(2)通过计算,请指出哪种种植方案获利最高?
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)设种蔬菜x人,种烟叶y人,则种小麦(20-x-y)人,由20名下岗职工在郊区承包50亩土地的关系建立方程求出其解即可;
(2)设获利为w元,由总利润=蔬菜的利润+烟叶的利润+小麦的利润就可以表示出w与x之间的关系式,由一次函数的性质就可以求出结论.
(2)设获利为w元,由总利润=蔬菜的利润+烟叶的利润+小麦的利润就可以表示出w与x之间的关系式,由一次函数的性质就可以求出结论.
解答:解:(1)设种蔬菜x人,种烟叶y人,则种小麦(20-x-y)人,根据题意,得
2x+3y+4(20-x-y)=50
解得y=30-2x,
∴20-x-y=x-10…(1分)
∵每种农作物都种∴
∴10<x<15…(1分)
∵x为种蔬菜的人数,需取整数
∴x的值为11,12,13,14,
∴有4种种植方案.
(2)设获利为w元
w=1100×2x+750×3y+600×4(20-x-y)…(1分)
=2200x+2250(30-2x)+2400(x-10)
即w=100x+23500…(1分)
∵k=100>0,
∴w随x的增大而增大
当x=14时,w=24900最大.
30-2x=2 x-10=4
∴当14人种28亩蔬菜,2人种6亩烟叶,4人种16亩小麦时,获利最高.
2x+3y+4(20-x-y)=50
解得y=30-2x,
∴20-x-y=x-10…(1分)
∵每种农作物都种∴
|
∴10<x<15…(1分)
∵x为种蔬菜的人数,需取整数
∴x的值为11,12,13,14,
∴有4种种植方案.
(2)设获利为w元
w=1100×2x+750×3y+600×4(20-x-y)…(1分)
=2200x+2250(30-2x)+2400(x-10)
即w=100x+23500…(1分)
∵k=100>0,
∴w随x的增大而增大
当x=14时,w=24900最大.
30-2x=2 x-10=4
∴当14人种28亩蔬菜,2人种6亩烟叶,4人种16亩小麦时,获利最高.
点评:本题考查了二元一次不定方程的解法的运用,一元一次不等式组的解法的运用,一次函数的解析式的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
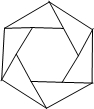 如图,把面积为a的正六边形的各边按同一方向延长,使延长的线段与原六边形的边长相等,顺次连接这六条线段的外端点可以得到一个新的正六边形,重复上述过程,经过6次后,所得正六边形的面积是( )
如图,把面积为a的正六边形的各边按同一方向延长,使延长的线段与原六边形的边长相等,顺次连接这六条线段的外端点可以得到一个新的正六边形,重复上述过程,经过6次后,所得正六边形的面积是( )| A、243a | ||
| B、729a | ||
| C、2187a | ||
D、243
|
 如图,等腰Rt△ABC的直角边长为2
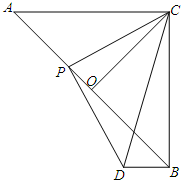
如图,等腰Rt△ABC的直角边长为2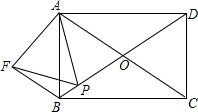 如图,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点P为线段BO上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP.
如图,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点P为线段BO上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP. 如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于点F,且∠CEF=2∠DAE.
如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于点F,且∠CEF=2∠DAE.
 如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为
如图,以矩形ABCD的顶点C为圆心作⊙C,⊙C分别交AB、CD于P、Q两点,当CB=2,CQ=4,CD=7时,阴影部分的面积为