题目内容
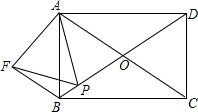 如图,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点P为线段BO上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP.
如图,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点P为线段BO上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP.考点:全等三角形的判定与性质,等边三角形的性质,矩形的性质
专题:证明题
分析:根据矩形的对角线互相平分且相等求出OA=OB,然后判断出△AOB是等边三角形,根据等边三角形的性质可得AB=AO,∠BAO=60°,根据等边三角形的性质可得AF=AP,∠FAP=60°,再求出∠BAF=∠OAP,然后利用“边角边”证明△ABF和△AOP全等,根据全等三角形对应边相等证明即可.
解答:证明:∵四边形ABCD是矩形,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO,∠BAO=60°,
∵△APF是等边三角形,
∴AF=AP,∠FAP=60°,
∴∠BAF+∠BAP=∠OAP+∠BAP=60°,
∴∠BAF=∠OAP,
在△ABF和△AOP中,
,
∴△ABF≌△AOP(SAS),
∴BF=OP.
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO,∠BAO=60°,
∵△APF是等边三角形,
∴AF=AP,∠FAP=60°,
∴∠BAF+∠BAP=∠OAP+∠BAP=60°,
∴∠BAF=∠OAP,
在△ABF和△AOP中,
|
∴△ABF≌△AOP(SAS),
∴BF=OP.
点评:本题考查了全等三角形的判定与性质,矩形的性质,等边三角形的判定与性质,熟记各性质并确定出全等的三角形和全等的条件是解题的关键.

练习册系列答案
相关题目
在算式(-
)□(-
)的□中填上运算符号,使结果最大的是( )
| ||
| 2014 |
| ||
| 2014 |
| A、加号 | B、减号 | C、乘号 | D、除号 |

 如图,E是矩形ABCD的边BC上的一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
如图,E是矩形ABCD的边BC上的一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H. 如图,已知直线y=mx+b与双曲线y=
如图,已知直线y=mx+b与双曲线y=
 如图,边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′,图中重合部分的面积为
如图,边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′,图中重合部分的面积为