题目内容
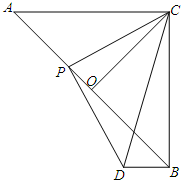 如图,等腰Rt△ABC的直角边长为2
如图,等腰Rt△ABC的直角边长为2| 2 |
(1)求证:
| PC |
| CD |
| CO |
| CB |
(2)请你判断AC与BD有什么位置关系?并说明理由.
(3)当点P在线段AB上运动时,设AP=x,△PBD的面积为S,求S与x之间的函数关系式.
考点:相似形综合题
专题:
分析:(1)根据△ABC为等腰直角三角形,可推出△BCO为等腰直角三角形,则
=
,再根据△PCD为等腰直角三角形,
得
=
,从而得出结论
=
;
(2)由(1)的结论可得出∠PCO=∠BCD,再由
=
,可证明△PCO∽△DCB,从而得出∠ABD=∠BAC,根据平行线的判定定理可得出AC∥BD;
(3)分两种情况讨论:①当点P在线段AO上时,作PE⊥BD,如图1,根据△ABC为等腰直角三角形,得AB=4,PO=2-x,BP=4-x,
可证明△PCO∽△DCB,得
=
,可得出BD=
(2-x),再得出PE=
(4-x),即可得出S与x的解析式S=
x2-3x+4;
②当点P在线段BO上时,作PE⊥BD,如图2,可知:OP=x-2,BP=4-x,再根据△PCO∽△DCB,可得
=
,得出BD=
(x-2),得PE=
(4-x),即可得出S与x的解析式S=-
x2+3x-4.
| OC |
| BC |
| ||
| 2 |
得
| PC |
| CD |
| ||
| 2 |
| PC |
| CD |
| CO |
| CB |
(2)由(1)的结论可得出∠PCO=∠BCD,再由
| PC |
| CD |
| CO |
| CB |
(3)分两种情况讨论:①当点P在线段AO上时,作PE⊥BD,如图1,根据△ABC为等腰直角三角形,得AB=4,PO=2-x,BP=4-x,
可证明△PCO∽△DCB,得
| CO |
| CB |
| PO |
| BD |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
②当点P在线段BO上时,作PE⊥BD,如图2,可知:OP=x-2,BP=4-x,再根据△PCO∽△DCB,可得
| CO |
| CB |
| PO |
| BD |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:解:(1)∵△ABC为等腰直角三角形,
∴O是AB的中点
∴∠OCB=∠CBO=45°,∠COB=∠AOC=90°,
∴△BCO为等腰直角三角形,
∴
=
,
∵△PCD为等腰直角三角形
∴∠PCD=45°,
=
,
∴
=
;
(2)由(1)可知:
∴∠PCO+∠OCD=∠BCD+∠OCD=45°,
∴∠PCO=∠BCD,
又∵
=
,
∴△PCO∽△DCB,
∴∠CBD=∠AOC=90°,
∴∠ABD=∠BAC=45°,
∴AC∥BD;
(3)分两种情况讨论:
①当点P在线段AO上时,
作PE⊥BD,如图1,
∵AC=BC=2
,△ABC为等腰直角三角形,
∴AB=2AO=2BO=4,
∴PO=2-x,BP=4-x,
∵△PCO∽△DCB,
∴
=
,
即:
=
,
∴BD=
(2-x),
∵∠PBE=45°,
∴PE=
(4-x),
∴S=
•
(2-x)•
(4-x)=
x2-3x+4,
②当点P在线段BO上时,
作PE⊥BD,如图2,
可知:OP=x-2,BP=4-x,
∵△PCO∽△DCB
∴
=
,
即:
=
,
∴BD=
(x-2),
∵∠PBE=45°,
∴PE=
(4-x),
∴S=
•
(x-2)•
(4-x)=-
x2+3x-4.
∴O是AB的中点
∴∠OCB=∠CBO=45°,∠COB=∠AOC=90°,
∴△BCO为等腰直角三角形,
∴
| OC |
| BC |
| ||
| 2 |
∵△PCD为等腰直角三角形
∴∠PCD=45°,
| PC |
| CD |
| ||
| 2 |
∴
| PC |
| CD |
| CO |
| CB |
(2)由(1)可知:
∴∠PCO+∠OCD=∠BCD+∠OCD=45°,
∴∠PCO=∠BCD,
又∵
| PC |
| CD |
| CO |
| CB |
∴△PCO∽△DCB,
∴∠CBD=∠AOC=90°,
∴∠ABD=∠BAC=45°,
∴AC∥BD;
(3)分两种情况讨论:
①当点P在线段AO上时,
作PE⊥BD,如图1,
∵AC=BC=2
| 2 |
∴AB=2AO=2BO=4,

∴PO=2-x,BP=4-x,
∵△PCO∽△DCB,
∴
| CO |
| CB |
| PO |
| BD |
即:
| 2 | ||
2
|
| 2-x |
| BD |
∴BD=
| 2 |
∵∠PBE=45°,
∴PE=
| ||
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
②当点P在线段BO上时,

作PE⊥BD,如图2,
可知:OP=x-2,BP=4-x,
∵△PCO∽△DCB
∴
| CO |
| CB |
| PO |
| BD |
即:
| 2 | ||
2
|
| x-2 |
| BD |
∴BD=
| 2 |
∵∠PBE=45°,
∴PE=
| ||
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查了相似形的综合题以及等腰三角形的性质、勾股定理和函数解析式的确定,是中考的重点,要认真把握每一个知识点及它们之间的联系.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
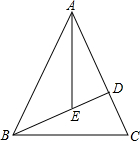 如图,在△ABC中,AB=AC=3,高BD=
如图,在△ABC中,AB=AC=3,高BD=

 如图,E是矩形ABCD的边BC上的一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
如图,E是矩形ABCD的边BC上的一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.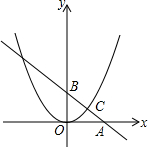 如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是
如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是