题目内容
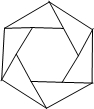 如图,把面积为a的正六边形的各边按同一方向延长,使延长的线段与原六边形的边长相等,顺次连接这六条线段的外端点可以得到一个新的正六边形,重复上述过程,经过6次后,所得正六边形的面积是( )
如图,把面积为a的正六边形的各边按同一方向延长,使延长的线段与原六边形的边长相等,顺次连接这六条线段的外端点可以得到一个新的正六边形,重复上述过程,经过6次后,所得正六边形的面积是( )| A、243a | ||
| B、729a | ||
| C、2187a | ||
D、243
|
考点:正多边形和圆,三角形的面积
专题:规律型
分析:先根据正六边形的性质得出∠1的度数,再根据AD=CD=BC判断出△ABC的形状及∠2的度数,求出AB的长,进而可得出,经过6次后,所得到的正六边形是原正六边形边长的倍数,然后根据面积比等于边长比的平方即可得到答案.
解答: 解:∵此六边形是正六边形,
解:∵此六边形是正六边形,
∴∠1=180°-120°=60°,
∵AD=CD=BC,
∴△BCD为等边三角形,
∴BD=
AC,
∴△ABC是直角三角形
又∵BC=
AC,
∴∠2=30°,
∴AB=
BC=
CD,
同理可得,经过2次后,所得到的正六边形是原正六边形边长(
)2=3倍,
∴经过6次后,所得到的正六边形是原正六边形边长的(
)6=27倍,
∴原正六边形的边长:现正六边形的边长之比=1:27,
∴面积之比为1:729,
∴经过6次后,所得正六边形的面积729a,
故选B.
 解:∵此六边形是正六边形,
解:∵此六边形是正六边形,∴∠1=180°-120°=60°,
∵AD=CD=BC,
∴△BCD为等边三角形,
∴BD=
| 1 |
| 2 |
∴△ABC是直角三角形
又∵BC=
| 1 |
| 2 |
∴∠2=30°,
∴AB=
| 3 |
| 3 |
同理可得,经过2次后,所得到的正六边形是原正六边形边长(
| 3 |
∴经过6次后,所得到的正六边形是原正六边形边长的(
| 3 |
∴原正六边形的边长:现正六边形的边长之比=1:27,
∴面积之比为1:729,
∴经过6次后,所得正六边形的面积729a,
故选B.
点评:本题考查的是正多边形和圆,解答此题的关键是熟知正多边形内角的性质及直角三角形的判定定理,此题有一定的难度.

练习册系列答案
相关题目
在算式(-
)□(-
)的□中填上运算符号,使结果最大的是( )
| ||
| 2014 |
| ||
| 2014 |
| A、加号 | B、减号 | C、乘号 | D、除号 |
已知
是二元一次方程组
的解,则a-b的值为( )
|
|
| A、-1 | B、1 | C、2 | D、3 |
若(a-2)2+|b-1|=0,则(b-a)2013的值是( )
| A、-l | B、0 | C、1 | D、2013 |
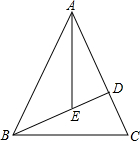 如图,在△ABC中,AB=AC=3,高BD=
如图,在△ABC中,AB=AC=3,高BD=