题目内容
6.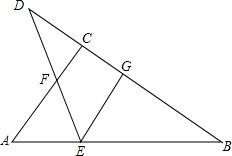 如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.
如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.
分析 先根据EG是线段BD的垂直平分线得出∠DEG=∠BEG,再由∠ACB=90°可知AC∥EG,故∠AFE=∠DEG,∠A=∠BEG,所以∠A=∠AFE,由此即可得出结论.
解答 证明:∵EG是线段BD的垂直平分线,
∴∠DEG=∠BEG,
∵∠ACB=90°,
∴AC∥EG,
∴∠AFE=∠DEG,∠A=∠BEG,
∴∠A=∠AFE,
∴△AEF是等腰三角形.
点评 本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
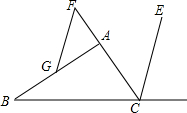 如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数.
如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数.
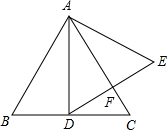 如图,在正△ABC中,AD⊥BC于点D,以AD为一边向右作正△ADE.请判断AC,DE的位置关系,并给出证明.
如图,在正△ABC中,AD⊥BC于点D,以AD为一边向右作正△ADE.请判断AC,DE的位置关系,并给出证明.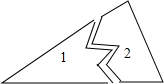 如图,一块三角形的玻璃破碎成如图的1、2两块,现在需要配同样大小的玻璃,为了方便,只需带上第②块,理由是:ASA.
如图,一块三角形的玻璃破碎成如图的1、2两块,现在需要配同样大小的玻璃,为了方便,只需带上第②块,理由是:ASA. 将一根长为6m的木条做成如图形状的长方形框架,设AB=x(m),要求x不能小于0.5m.
将一根长为6m的木条做成如图形状的长方形框架,设AB=x(m),要求x不能小于0.5m.