题目内容
18.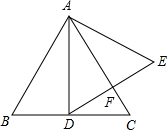 如图,在正△ABC中,AD⊥BC于点D,以AD为一边向右作正△ADE.请判断AC,DE的位置关系,并给出证明.
如图,在正△ABC中,AD⊥BC于点D,以AD为一边向右作正△ADE.请判断AC,DE的位置关系,并给出证明.
分析 根据等边三角形的性质求得∠C=∠ADE=60°,根据三角形的内角和于是得到∠CFD=30°,从而判断∠CFD=90°即可.
解答 解:AC、DE的位置关系:AC⊥DE.
∵△ABC和△ADE是等边三角形,
∴∠C=60°,∠ADE=60°,
∵AD⊥BC,
∴∠ADC=90°,
在△CDF中,∵∠CDE=90°-∠ADE=30°,
∴∠CFD=180°-∠C-∠CDE=180°-60°-30°=90°.
∴AC⊥DE.
点评 本题考查了正三角形的性质以及垂直的定义,解决的关键是对这些基本性质的理解和掌握.

练习册系列答案
相关题目
7.把连续奇数列成下表:
(1)表中的m值是19:
(2)第6行、第5列的数字是65;
(3)请用一个长方形方框框住表中的四个数字,交叉相乘,再将乘积相减.看看你能发现什么结论,用文字语言表述你的结论.并用整式运算证明你的结论.
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | 第六列 | 第七列 | |
| 第1行 | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 第2行 | 15 | 17 | m | 21 | 23 | 25 | 27 |
| 第3行 | 29 | 31 | 33 | 35 | 37 | 39 | 41 |
| 第4行 | 43 | 45 | 47 | 49 | 51 | 53 | 55 |
| … |
(2)第6行、第5列的数字是65;
(3)请用一个长方形方框框住表中的四个数字,交叉相乘,再将乘积相减.看看你能发现什么结论,用文字语言表述你的结论.并用整式运算证明你的结论.
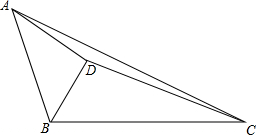 如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.
如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.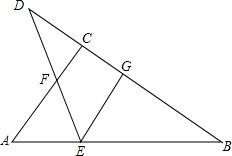 如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.
如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.
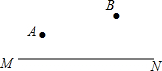 直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)
直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)