题目内容
17．二次函数y=ax2+bx+c顶点为（2，8），与x轴一个交点的横坐标为-2，求它的函数关系式．分析 设出抛物线的顶点式，然后代入（-2，0），根据待定系数法即可求得．
解答 解：∵二次函数y=ax2+bx+c顶点为（2，8），
∴设二次函数的解析式为y=a（x-2）2+8，
把（2，0）代入得0=a（-2-2）2+8，
∴a=-$\frac{1}{2}$，
∴它的函数关系式为y=（x-2）2+8．
点评 本题考查了待定系数法求二次函数的解析式，熟练掌握待定系数法是解题的关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
7．某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小明已根据成绩表算出了甲成绩的平均数和方差，请你完成下面两个问题．
甲、乙两人射箭成绩统计表
小明的正确计算：$\overline{{x}_{甲}}$=$\frac{1}{5}$（9+4+7+6）=6（环），s甲2=$\frac{1}{5}$[（9-6）2+（4-6）2+（7-6）2+（4-6）2+（6-6）2]=3.6（环2）
（1）求m的值和乙的平均数及方差；
（2）请你从平均数和方差的角度分析，谁将被选中．
甲、乙两人射箭成绩统计表
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲成绩 | 9 | 4 | 7 | 4 | 6 |
| 乙成绩 | 7 | 5 | 7 | m | 7 |
（1）求m的值和乙的平均数及方差；
（2）请你从平均数和方差的角度分析，谁将被选中．
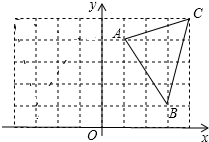如图，平面直角坐标系，已知A（1，4），B（3，1），C（4，5）．△ABC关于y轴的对称图形为△A1B1C1
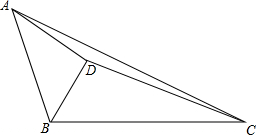如图，△ABC中，BD平分∠ABC，AD垂直于BD，△BCD的面积为45，△ADC的面积为20，求△ABD的面积．
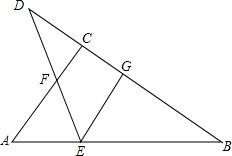如图，在△ABC中，∠ACB=90°，D是BC延长线上一点，E是BD的垂直平分线EG与AB的交点，连接DE交AC于点F．试说明：△AEF是等腰三角形．
7．把连续奇数列成下表：
（1）表中的m值是19：
（2）第6行、第5列的数字是65；
（3）请用一个长方形方框框住表中的四个数字，交叉相乘，再将乘积相减．看看你能发现什么结论，用文字语言表述你的结论．并用整式运算证明你的结论．
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | 第六列 | 第七列 | |
| 第1行 | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| 第2行 | 15 | 17 | m | 21 | 23 | 25 | 27 |
| 第3行 | 29 | 31 | 33 | 35 | 37 | 39 | 41 |
| 第4行 | 43 | 45 | 47 | 49 | 51 | 53 | 55 |
| … |
（2）第6行、第5列的数字是65；
（3）请用一个长方形方框框住表中的四个数字，交叉相乘，再将乘积相减．看看你能发现什么结论，用文字语言表述你的结论．并用整式运算证明你的结论．