题目内容
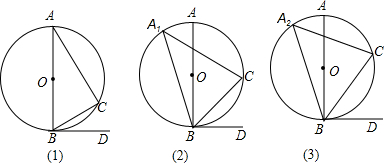
14.如图,AB是⊙O的直径,C为圆周上一点,BD是⊙0的切线,B为切点.(1)在图(1)中,∠BAC=30°,求∠DBC的度数;
(2)在图(2)中,∠BA1C=40°,求∠DBC的度数;
(3)在图(3)中,∠BA2C=α,求∠DBC的度数;
(4)通过(1)(2)(3)的探究你发现了什么?用你自己的语言叙述你的发现.
分析 (1)由切线的性质和圆周角定理以及角的互余关系得出∠DBC=∠A=30°即可;
(2)连接AC,由(1)得出∠DBC=∠A,由圆周角定理得出∠A=∠A1,即可得出∠DBC=∠BA1C=40°;
(3)由(2)得出∠DBC=∠BA2C=α即可;(4)∠DBC等于$\widehat{BC}$所对的圆周角,得出弦切角定理.
解答 解:(1)∵BD是⊙0的切线,
∴∠ABO=90°,
即∠ABC+∠DBC=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠DBC=∠A=30°;
(2)连接AC,如图所示:
由(1)得:∠DBC=∠A,
又∵∠A=∠A1,
∴∠DBC=∠BA1C=40°;
(3)由(2)得:∠DBC=∠BA2C=α;
(4)∠DBC等于$\widehat{BC}$所对的圆周角;
弦切角等于它夹的弧所对的圆周角.
点评 本题考查了圆周角定理、弦切角定理;熟练掌握圆周角定理是解决问题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
5.关于矩形性质,下列说法不正确的是( )
| A. | 四个角都是直角 | |
| B. | 既是轴对称图形,也是中心对称图形 | |
| C. | 对角线互相垂直 | |
| D. | 对角线互相平分且相等 |
 如图请分别画出它的三视图.
如图请分别画出它的三视图. 如图,平面直角坐标系,已知A(1,4),B(3,1),C(4,5).△ABC关于y轴的对称图形为△A1B1C1
如图,平面直角坐标系,已知A(1,4),B(3,1),C(4,5).△ABC关于y轴的对称图形为△A1B1C1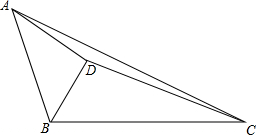 如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.
如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.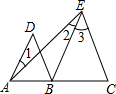 根据下列证明过程填空:
根据下列证明过程填空: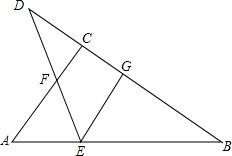 如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.
如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.