题目内容
1.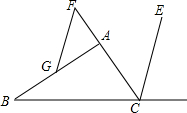 如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数.
如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,求∠BAC的度数.
分析 根据角平分线的定义求出∠ACE,再根据两直线平行,内错角相等可得∠AFG=∠ACE,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BAC.
解答 解:∵CE平分∠ACD,
∴∠ACE=$\frac{1}{2}$×∠ACD=$\frac{1}{2}$×100°=50°,
∵FG∥CE,
∴∠AFG=∠ACE=50°,
在△AFG中,∠BAC=∠AFG+∠AGF=50°+20°=70°.
点评 本题考查了三角形的内角和定理,角平分线的定义,平行线的性质,以及三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
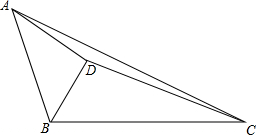 如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.
如图,△ABC中,BD平分∠ABC,AD垂直于BD,△BCD的面积为45,△ADC的面积为20,求△ABD的面积.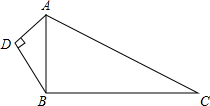 如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.
如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.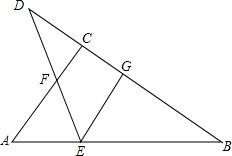 如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.
如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线EG与AB的交点,连接DE交AC于点F.试说明:△AEF是等腰三角形.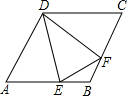 如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.
如图,在菱形ABCD中,点E、F分别是AB和BC上的点,且BE=BF,求证:△ADE≌△CDF.