题目内容
12.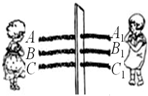 如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.(1)问:“姐妹两人同时选中同一根绳子”这一事件是随机事件,概率是$\frac{1}{3}$;
(2)在互相看不见的条件下,姐姐先将左侧A、C两个绳端打成一个连结,则妹妹从右侧A1、B1、C1三个绳端中随机选两个打一个结(打结后仍能自由地通过木孔);请求出“姐姐抽动绳端B,能抽出由三根绳子连结成一根长绳”的概率是多少?
分析 (1)由三根同样的绳子AA1、BB1、CC1穿过一块木板,直接利用概率公式求解即可求得答案;
(2)利用列举法可得:ACA1B1,ACA1C1,ACB1C1,其中符合题意的有2种(ACA1B1、ACB1C1),然后直接利用概率公式求解即可求得答案.
解答 解:(1)∵共有三根同样的绳子AA1、BB1、CC1穿过一块木板,
∴姐妹两人同时选中同一根绳子的概率是:$\frac{1}{3}$,这一事件是随机事件;
故答案为:随机,$\frac{1}{3}$;
(2)列举得:ACA1B1,ACA1C1,ACB1C1;
∴共有3种等可能的结果,其中符合题意的有2种(ACA1B1、ACB1C1),
∴能抽出由三根绳子连结成一根长绳”的概率是:$\frac{2}{3}$.
点评 此题考查了列举法求概率的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.在一个圆中,给出下列命题,其中正确的是( )
| A. | 若圆心到两条直线的距离都等于圆的半径,则这两条直线不可能垂直 | |
| B. | 若圆心到两条直线的距离都小于圆的半径,则这两条直线与圆一定有四个公共点 | |
| C. | 若两条弦所在直线平行,则这两条弦之间的距离一定小于圆的直径 | |
| D. | 若两条弦所在直线不平行,则这两条弦一定在圆内有公共点 |
1.下列事件是必然事件的是( )
| A. | 若a>b,则ac<bc | |
| B. | 在常规情况下,将水加热到100℃时水会沸腾 | |
| C. | 投掷一枚硬币,落地后正面朝上 | |
| D. | 长为3cm、3cm、7cm的三条线段能围成一个三角形 |
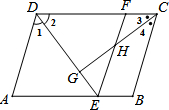 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).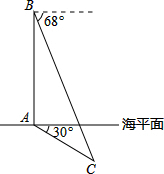 我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)
我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)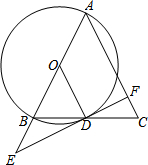 如图,AB是⊙O的直径,以AB为边作△ABC,使得AC=AB,BC交⊙O于点D,联结OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.
如图,AB是⊙O的直径,以AB为边作△ABC,使得AC=AB,BC交⊙O于点D,联结OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.