题目内容
20.(1)化简:(a+3)2+a(4-a)(2)计算:(1-$\sqrt{3}$)0+|-$\sqrt{2}$|-2cos45°+($\frac{1}{4}$)-1
(3)解方程:x2-3x-1=0
(4)解不等式组:$\left\{\begin{array}{l}{5x-12≤2(4x-3)}\\{\frac{3x-1}{2}<1}\end{array}\right.$.
分析 (1)原式利用完全平方公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(2)原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用特殊角的三角函数值计算,最后一项利用负指数幂法则计算即可得到结果;
(3)方程利用公式法求出解即可;
(4)找出不等式组中两不等式的解集的公共部分即可.
解答 解:(1)原式=a2+6a+9+4a-a2=10a+9;
(2)原式=1+$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$+4=5;
(3)这里a=1,b=-3,c=-1,
∵△=9+4=13,
∴x=$\frac{3±\sqrt{13}}{2}$;
(4)$\left\{\begin{array}{l}{5x-12≤2(4x-3)①}\\{\frac{3x-1}{2}<1②}\end{array}\right.$,
由①得:x≥-2,
由②得:x<1,
则不等式的解集为-2≤x<1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.中华人民共和国的陆地面积为9600000km2,9600000这个数用科学记数法表示为( )
| A. | 9.6×105 | B. | 96×105 | C. | 9.6×106 | D. | 96×106 |
11.A、B两家工厂生产同一型号的电池,现分别抽取了6节电池,测试连续使用时间,结果如表:
(1)计算两组数据的总和及平均数,并填表;
(2)哪家生产的电池质量更好一些?
| 项目 | 1 | 2 | 3 | 4 | 5 | 6 | 总和/h | 平均数/h |
| A厂家电池使用时间/h | 40 | 48 | 40 | 42 | 43 | 45 | ||
| B厂家电池使用时间/h | 40 | 50 | 45 | 46 | 46 | 52 |
(2)哪家生产的电池质量更好一些?
5.已知a、b是一元次方程x2-2x-3=0的两个根,则a2b+ab2的值是( )
| A. | -1 | B. | -5 | C. | -6 | D. | 6 |
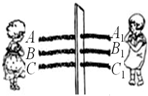 如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.