题目内容
2.水平地面上的甲,乙两楼的距离为30米,从甲楼顶部测得乙楼顶部的仰角为30°,测得乙楼底部的俯角为45°.求甲乙两楼的高度.分析 因为BD=30米,所以可通过三角函数关系分别求出DE和CE,进而可求的CD的高度.
解答 解:根据题意:AE⊥CD,∠CAE=30°,∠DAE=45°,AE=BD=30m,
在Rt△ACE中,CE=AEtan30°=30×$\frac{\sqrt{3}}{3}$=10$\sqrt{3}$(m),
在Rt△ADE中,DE=AE•tan45°=30×1=30,
∴乙楼的高为:CD=CE+DE=(10$\sqrt{3}$+30)m.
点评 本题考查解直角三角形的应用--仰角俯角问题,要注意利用已知线段和角通过三角关系求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若关于y的一元二次方程ky2-7y-7=0有实根,则k的取值范围是( )
| A. | k>-$\frac{7}{4}$ | B. | k≥-$\frac{7}{4}$且k≠0 | C. | k≤-$\frac{7}{4}$ | D. | k>-$\frac{7}{4}$且k≠0 |
7.计算:2000-2015=( )
| A. | 2000 | B. | -2015 | C. | 15 | D. | -15 |
14. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:
①abc<0;②b2-4ac>0;③3a+c>0;④(a+c)2<b2,其中正确的结论为( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③3a+c>0;④(a+c)2<b2,其中正确的结论为( )
| A. | ①② | B. | ②④ | C. | ①③④ | D. | ①③ |
11.将直角坐标系中的点(-1,-3)向上平移4个单位,再向右平移2个单位后的点的坐标为( )
| A. | (3,-1) | B. | (-5,-1) | C. | (-3,1) | D. | (1,1) |
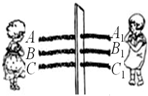 如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.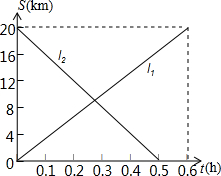 甲、乙两辆摩托车分别从A、B两地同时出发相向而行,两辆摩托车与A地的距离S(km)与行驶时间t(min)之间的函数关系如图,则下列说法中正确的有( )
甲、乙两辆摩托车分别从A、B两地同时出发相向而行,两辆摩托车与A地的距离S(km)与行驶时间t(min)之间的函数关系如图,则下列说法中正确的有( )