题目内容
17.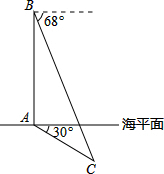 我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)
我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)
分析 过点C作CD⊥AB,交BA的延长线于点D,则AD就是潜艇C的下潜深度.设AD=x,则BD=BA+AD=1000+x,在Rt△ACD中,列出1000+x=$\sqrt{3}$x•tan68°即可解答.
解答 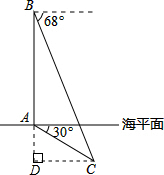 解:如图,过点C作CD⊥AB,交BA的延长线于点D,则AD就是潜艇C的下潜深度.由题意,得∠ACD=30°,∠BCD=68°.设AD=x,则BD=BA+AD=1000+x,
解:如图,过点C作CD⊥AB,交BA的延长线于点D,则AD就是潜艇C的下潜深度.由题意,得∠ACD=30°,∠BCD=68°.设AD=x,则BD=BA+AD=1000+x,
在Rt△ACD中,CD=$\frac{AD}{tan∠ACD}$=$\frac{x}{tan30°}$=$\sqrt{3}$x,在Rt△BCD中,BD=CD•tan68°,
∴1000+x=$\sqrt{3}$x•tan68°.
∴x=$\frac{1000}{\sqrt{3}tan68°}$≈$\frac{1000}{1.7×25-1}$≈308.
∴潜艇C的下潜深度约为308米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角、俯角构造直角三角形并解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知a、b是一元次方程x2-2x-3=0的两个根,则a2b+ab2的值是( )
| A. | -1 | B. | -5 | C. | -6 | D. | 6 |
7.计算:2000-2015=( )
| A. | 2000 | B. | -2015 | C. | 15 | D. | -15 |
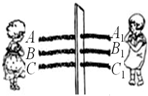 如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.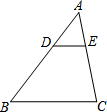 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,如果$\frac{AD}{DB}$=$\frac{3}{5}$,AE=6,那么EC的长为10.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,如果$\frac{AD}{DB}$=$\frac{3}{5}$,AE=6,那么EC的长为10.