题目内容
16. 过等腰△ABC底边BC上一点P引PM∥CA交AB于M;引PN∥BA交AC于N,作点P关于MN的对称点P′.试证:P′点在△ABC外接圆上,且P′B:P′C=BP:PC.
过等腰△ABC底边BC上一点P引PM∥CA交AB于M;引PN∥BA交AC于N,作点P关于MN的对称点P′.试证:P′点在△ABC外接圆上,且P′B:P′C=BP:PC.
分析 根据平行得到的同位角相等可得PM=BM,利用轴对称的选择可得PM=P′M,同理可得NP′=NP=NC,那么点M是△P′BP的外心,点N是△P′PC的外心,进而证明∠BP′C=∠BAC,可得P′点在△ABC外接圆上,根据圆周角定理得到P′P平分∠BP′C,然后根据三角形角平分线定理即可得到结论.
解答 解:连接P′M,P′N,PP′,
∵点P关于MN的对称点为P′.
∴MP′=MP=MB,NP′=NP=NC,
∴点M是△P′BP的外心,点N是△P′PC的外心,
∴∠BP′P=$\frac{1}{2}$∠BMP=$\frac{1}{2}$∠BAC,
∠PP′C=$\frac{1}{2}$∠PNC=$\frac{1}{2}$∠BAC.
∴∠BP′C=∠BP′P+∠P′PC=∠BAC.
从而,P′点与A,B,C共圆,
即P′在△ABC外接圆上;
∵PM∥AC,PN∥AB,
∴∠MPB=∠ABC=∠NPC=∠ACB=60°,
∴△PBM与△PCN是等边三角形.
∴∠BMP=∠CNP=60°,
∴∠BP′P=∠CP′P=30°,
∴P′P平分∠BP′C,
∴P′B:P′C=BP:PC.
点评 本题考查了三角形的外接圆和外心,三角形的角平分线定理,四点共圆,熟练掌握三角形的角平分线定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.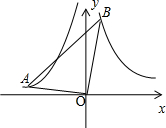 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
 如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )
如图,∠AOB=90°,且OA、OB分别与函数y=-$\frac{2}{x}$(x<0)、y=$\frac{3}{x}$(x>0)的图象交于A、B两点,则tan∠OBA的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3}{2}$ |
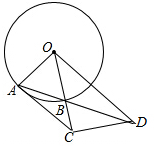 已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.
已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.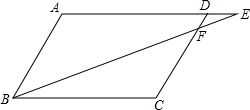 如图,在?ABCD中,E为AD的延长线上的点.求证:
如图,在?ABCD中,E为AD的延长线上的点.求证: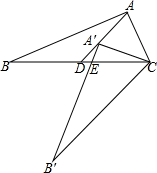 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.
如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE=4:3.