题目内容
11.点P为正三角形ABC内一点,PA=a,PB=b,PC=c,试用a、b、c表示S△ABC.分析 将△PAB绕点B顺时针旋转60°到△DCB,所以△PAB与△PBC的面积和就是四边形PBDC,也就是正△PBD与△PDC的面积和,利用海伦公式可得△PDC的面积,易得四边形PBDC的面积,同理可得四边形PCEA、四边形PAFB的面积,将这三个四边形的面积相加就是△ABC面积的2倍,易得结论.
解答 解:将△PAB绕点B顺时针旋转60°到△DCB
所以△PAB与△PBC的面积和就是四边形PBDC,也就是正△PBD与△PDC的面积和,
正△PBD是以b为边,面积为$\frac{{\sqrt{3}b}^{2}}{4}$,
△PDC的面积根据海伦公式得,S△PDC=$\sqrt{[s(s-a)(s-b)(s-c)]}$,
所以S四边形PBDC=$\frac{\sqrt{3}}{4}$b2+$\sqrt{[s(s-a)(s-b)(s-c)]}$,
同理可得S四边形PCEA=$\frac{\sqrt{3}}{4}$c2+$\sqrt{[s(s-a)(s-b)(s-c)]}$,
S四边形PAFB=$\frac{\sqrt{3}}{4}$a2+$\sqrt{[s(s-a)(s-a)(s-a)]}$,
将这三个四边形的面积相加就是△ABC面积的2倍,
所以S△ABC=$\frac{\sqrt{3}}{2}$(a2+b2+c2)$+\frac{3}{2}$$\sqrt{[s(s-a)(s-b)(s-c)]}$
其中s=$\frac{1}{2}$(a+b+c).
点评 本题主要考查了等边三角形的性质,利用海伦公式三角形的面积等于$\sqrt{s(s-a)(s-b)(s-c)}$其中s=$\frac{1}{2}$(a+b+c)是解答此题的关键.

练习册系列答案
相关题目
2.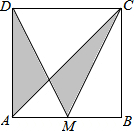 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
20.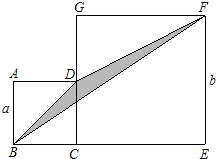 四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )
四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )
 四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )
四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为a,正方形CEFG的边长为b,连接BD,BF和DF后得到三角形BDF,请用含字母a和b的代数式表示三角形BDF的面积可表示为( )| A. | ab | B. | $\frac{1}{2}$ab | C. | $\frac{1}{2}$b2 | D. | $\frac{1}{2}$a2 |
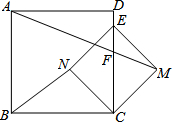 如图,在正方形ABCD中,E为CD边上一点,以CE为对角线构造正方形CMEN,点N在正方形ABCD内部,连接AM,与CD边交于点F.若CF=3,DF=2,连接BN,则BN的长为$\frac{25}{7}$.
如图,在正方形ABCD中,E为CD边上一点,以CE为对角线构造正方形CMEN,点N在正方形ABCD内部,连接AM,与CD边交于点F.若CF=3,DF=2,连接BN,则BN的长为$\frac{25}{7}$. 如图,BD:DC=3:5,F是AD中点,那么S△AEF:S△FDC=3:13..
如图,BD:DC=3:5,F是AD中点,那么S△AEF:S△FDC=3:13.. 过等腰△ABC底边BC上一点P引PM∥CA交AB于M;引PN∥BA交AC于N,作点P关于MN的对称点P′.试证:P′点在△ABC外接圆上,且P′B:P′C=BP:PC.
过等腰△ABC底边BC上一点P引PM∥CA交AB于M;引PN∥BA交AC于N,作点P关于MN的对称点P′.试证:P′点在△ABC外接圆上,且P′B:P′C=BP:PC. 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转20°.


