题目内容

20．已知方程组$\left\{\begin{array}{l}{ax+by=2}\\{bx+ay=4}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$，则a+b的值为（　　）
A．1B．2C．3D．4

分析 根据方程组的解的概念，将x、y的值代入原方程组从而得到关于a、b的二元一次方程组，观察到a、b系数特点，将两方程相加后除以3即可得答案．

解答 解：将$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{ax+by=2}\\{bx+ay=4}\end{array}\right.$，得：$\left\{\begin{array}{l}{2a+b=2}&{①}\\{2b+a=4}&{②}\end{array}\right.$，
①+②，得：3a+3b=6，即a+b=2，
故选：B．

点评 本题主要考查二元一次方程组的解的概念，理解并掌握满足方程组中每个方程的未知数的值即为方程组的解是根本．

练习册系列答案
相关题目
10．若点（-2，y1），（-1，y2）（1，y3）在反比例函数y=$-\frac{2}{x}$的图象上，则下列结论正确的是（　　）
A．y1＞y2＞y3B．y2＞y1＞y3C．y3＞y1＞y2D．y3＞y2＞y1
11．多项式x2y-2x2y3+3x3y的公因式是x2y．
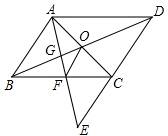8．如图，在?ABCD中，F是边BC的中点，连接AF交DC的延长线于点E，AC，BD相交于点O，AF交BD于点G，连接OF，判断EC与OF的位置关系和大小关系，并证明你的结论．
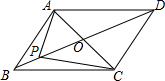15．如图，已知四边形ABCD是平行四边形，点O为对角线AC、BD的交点
（1）求证：S△AOB=S△BOC；
（2）设P为对角线BD上任意一点（点P与点B、D不重合），试猜想S△APB与S△BPC的大小关系，并说明理由．
5．已知，A是反比例函数y=$\frac{k}{x}$的图象上的一点，AB⊥x轴于点B，O是坐标原点，且△ABO的面积是3，则k的值是（　　）
A．3B．±3C．6D．±6
12．如图已知，OM平分∠AOB，点D，C分别在OM，OA上，∠COD=∠CDO，求证：CD∥OB．
9．下列方程中，属于一元二次方程的是（　　）
A．$\frac{1}{{x}^{2}}+\frac{1}{x}-3=0$B．ax2+bx+c=0C．x2+5x=x2-3D．x2-3x+2=0
10．如图，矩形OABC的顶点A、C的坐标分别为（0，10）、（4，0），反比例函数y=$\frac{k}{x}（k≠0）$在第一象限内的图象过矩形OABC的对角线的交点M，并与AB、BC分别交于点E、F，连接OE、EF、OF，则△OEF的面积为$\frac{75}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网