题目内容
4．用代数式表示：①甲数比乙数的2倍多4，设甲数为x，则乙数为$\frac{x-4}{2}$；②甲数与乙数的和是10，设甲数为y，则乙数为10-y．分析 ①甲数x=2个乙数+4，从而得出乙数；
②乙数=和-甲数．
解答 解：根据题意得：①$\frac{x-4}{2}$；②10-y；
故答案为：$\frac{x-4}{2}$；10-y．
点评 本题考查了列代数式，比较简单，列代数式时，要先认真审题，抓住关键词语，并注意书写的规范性．
练习册系列答案
相关题目
实数a，b在数轴上的位置如图所示，且|a|＞|b|，化简：$\sqrt{{a}^{2}}$-$\sqrt{（a+b）^{2}}$=b．
12．十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式请你观察下列几种简单多面体模型，解答下列问题：
（1）根据上面多面体的模型及表格中的数据：
你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是V+F-E=2；
（2）一个多面体每个顶点处都有3条棱，多面体的棱数比顶点数大10，则这个多面体的面数是12；
（3）某个玻璃饰品的外形是简单的多面体，它的外表面是由三角形和八边形两种多边形拼接而成，每个顶点处都有3条棱，共有棱36条．若该多面体外表面三角形的个数比八边形的个数的2倍多2，求该多面体外表面三角形的个数．
（1）根据上面多面体的模型及表格中的数据：
| 多面体 | 顶点数（V） | 面数（F） | 棱数（E） |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
（2）一个多面体每个顶点处都有3条棱，多面体的棱数比顶点数大10，则这个多面体的面数是12；
（3）某个玻璃饰品的外形是简单的多面体，它的外表面是由三角形和八边形两种多边形拼接而成，每个顶点处都有3条棱，共有棱36条．若该多面体外表面三角形的个数比八边形的个数的2倍多2，求该多面体外表面三角形的个数．
19．
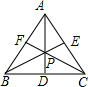在△ABC中，∠B、∠C平分线的交点P恰好在BC边的高AD上，则△ABC一定是（ ）
在△ABC中，∠B、∠C平分线的交点P恰好在BC边的高AD上，则△ABC一定是（ ）| A． | 直角三角形 | B． | 等边三角形 | C． | 等腰直角三角形 | D． | 等腰三角形 |
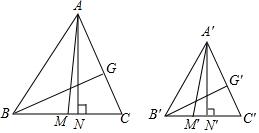
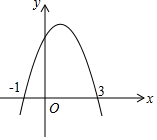如图，抛物线y=ax2+bx+c交x轴于（-1，0）、（3，0）两点，以下四个结论正确的是（用序号表示）（1）（2）（3）．
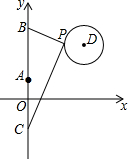如图，在平面直角坐标系中，已知点A（0，1）、点B（0，1+t）、C（0，1-t）（t＞0），点P在以D（3，3）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则t的最小值是$\sqrt{13}$-1．
如图，△ABC中，∠AED=∠B，AD=2，DB=4，AE=3，则EC=1．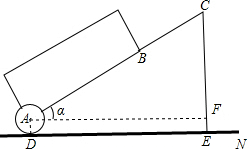
拉杆箱是人们出行的必需品，采用拉杆箱可以让我们的出行更轻松，如图，已知某种拉杆箱箱体长AB=50cm，拉杆最大伸长距离BC=40cm，点A到地面的距离AD=8cm，拉杆箱与水平面的夹角α的度数为35°．（提示：sin35°≈0.57，cos35°≈0.82）．