题目内容
14.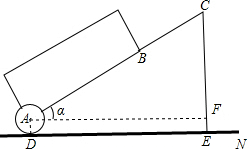 拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).
拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).(1)当拉杆伸到最长距离时,求该拉杆箱底部A到拉杆把手C处的水平距离AF;
(2)当拉杆伸到最长距离时,求该拉杆把手C处到地面的距离CE.
分析 (1)直接利用锐角三角函数关系得出AF的长即可;
(2)直接利用锐角三角函数关系得出CF的长,进而求出EC的长.
解答  解:(1)由题意可得:AC=AB+BC=50+40=90(cm),
解:(1)由题意可得:AC=AB+BC=50+40=90(cm),
则cos35°=$\frac{AF}{AC}$=$\frac{AF}{90}$,
故AF≈90×0.82=73.8(cm),
答:该拉杆箱底部A到拉杆把手C处的水平距离AF为73.8cm;
(2)由题意可得:sin35°=$\frac{FC}{AC}$=$\frac{FC}{90}$,
则FC≈90×0.57=51.3(cm),
故EC=FC+FE=59.3(cm),
答:该拉杆把手C处到地面的距离CE为59.3cm.
点评 此题主要考查了解直角三角形的应用,正确选择三角函数关系是解题关键.

练习册系列答案
相关题目
5.九年级某班部分同学利用课外活动时间,积极参加篮球定点投篮的训练,训练后的测试成绩如下表所示:
回答下列问题:
(1)训练后篮球定点投篮进球数的众数是4个,中位数是5个;
(2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数.
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定点投篮进球数的众数是4个,中位数是5个;
(2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数.
4.罗山西亚丽宝超市第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的$\frac{1}{2}$倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
(1)罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
| 甲 | 乙 | |
| 进价(元/件) | 20 | 30 |
| 售价(元/件) | 29 | 40 |
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.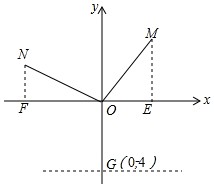 如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.
如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.