题目内容
19.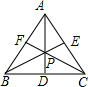 在△ABC中,∠B、∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )
在△ABC中,∠B、∠C平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )| A. | 直角三角形 | B. | 等边三角形 | C. | 等腰直角三角形 | D. | 等腰三角形 |
分析 先根据角平分线的性质判断出AD是△ABC的角平分线,然后利用“角边角”证明△ABD和△ACD全等,根据全等三角形对应边相等可得AB=AC,从而证明△ABC一定是等腰三角形.
解答 解:
∵∠ABC与∠ACB的平分线的交点P恰好在BC边的高AD上,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{∠BAD=∠CAD}\\{AD=AD}\\{∠ADB=∠ADC=90°}\end{array}\right.$,
∴△ABD≌△ACD(ASA),
∴AB=AC,
∴△ABC一定是等腰三角形.
故选D.
点评 本题主要考查等腰三角形的判定,利用角平分线的性质证得△ABD≌△ACD是解题的关键.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 三角形的外切圆有且只有一个 | |
| B. | 三角形的外心到这个三角形的三边距离相等 | |
| C. | 相等的圆心角所对的弧相等 | |
| D. | 等弧所对的圆心角相等 |
14.如果m÷n=12.其中m,n都是正整数,那么它们的最小公倍数是( )
| A. | m | B. | n | C. | 12 | D. | m与n的积 |
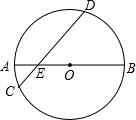 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.