题目内容
16.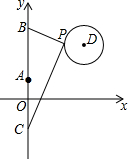 如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1-t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是$\sqrt{13}$-1.
如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1-t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是$\sqrt{13}$-1.
分析 先求出AB,AC进而得出AC=AB,结合直角三角形的斜边的中线等于斜边的一半,即AP=t,即可得出t最小时,点P在AD上,用两点间的距离公式即可得出结论.
解答 解:如图, 连接AP,
连接AP,
∵点A(0,1)、点B(0,1+t)、C(0,1-t)(t>0),
∴AB=(1+t)-1=t,AC=1-(1-t)=t,
∴AB=AC,
∵∠BPC=90°,
∴AP=$\frac{1}{2}$BC=AB=t,
要t最小,就是点A到⊙D上的一点的距离最小,
∴点P在AD上,
∵A(0,1),D(3,3),
∴AD=$\sqrt{9+(3-1)^{2}}$=$\sqrt{13}$,
∴t的最小值是AP=AD-PD=$\sqrt{13}$-1,
故答案为$\sqrt{13}$-1.
点评 此题主要考查了直角三角形斜边的中线的性质,平面坐标系内,两点间的距离公式,极值的确定;判断出点A是BC的中点是解本题的关键.是一道基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
6.在表中,我们把第i行第j列的数记为ai,j(其中i,j都是不大于4的正整数),对于表中的每个数ai,j,规定如下:当i>j时,ai,j=0;当i≤j时,ai,j=1.
例如:当i=4,j=1时,ai,j=a4,1=0.
(1)按此规定a1,3=1;
(2)请从下面两个问题中任选一个作答.
例如:当i=4,j=1时,ai,j=a4,1=0.
| a1,1 | a1,2 | a1,3 | a1,4 |
| a2,1 | a2,2 | a2,3 | a2,4 |
| a3,1 | a3,2 | a3,3 | a3,4 |
| a4,1 | a4,2 | a4,3 | a4,4 |
(2)请从下面两个问题中任选一个作答.
| 问题1 | 问题2 |
| a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0或3; | 表中的16个数中,共有10个1. |
5.九年级某班部分同学利用课外活动时间,积极参加篮球定点投篮的训练,训练后的测试成绩如下表所示:
回答下列问题:
(1)训练后篮球定点投篮进球数的众数是4个,中位数是5个;
(2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数.
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)训练后篮球定点投篮进球数的众数是4个,中位数是5个;
(2)若训练后的人均进球数比训练前增加25%,求训练前的人均进球数.
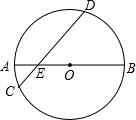 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点E,∠AEC=30°,OE:AE=2:3,求弦CD的长. 如图,△ABC是等腰三角形,∠BAC=90°,D为BC延长线上一点,连续AD,以AD为边在AD右侧作正方形ADEF,连续FC、EC,若AC=$\sqrt{2}$,AD=$\sqrt{10}$.
如图,△ABC是等腰三角形,∠BAC=90°,D为BC延长线上一点,连续AD,以AD为边在AD右侧作正方形ADEF,连续FC、EC,若AC=$\sqrt{2}$,AD=$\sqrt{10}$.