题目内容
1. 如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离.
如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离.
分析 由题意知,△BAC为直角三角形,在直角三角形中运用勾股定理求解.
解答 解:由题设可知∠BAC=90°,AB=6×2=12(海里),AC=8×2=16(海里),
由股定理得BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=20(海里).
答:B、C两岛的距离为20海里.
点评 本题考查了直角三角形中勾股定理的运用,解本题的关键是正确的运用勾股定理求解.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
12.某服装店用10000元购进一批某品牌夏季衬衫若干件,很快售完;该店又用14700元钱购进第二批这种衬衫,所进件数比第一批多40%,每件衬衫的进价比第一批每件衬衫的进价多10元,求第一批购进多少件衬衫?设第一批购进x件衬衫,则所列方程为( )
| A. | $\frac{10000}{x}$-10=$\frac{14700}{(1+40%)x}$ | B. | $\frac{10000}{x}$+10=$\frac{14700}{(1+40%)x}$ | ||
| C. | $\frac{10000}{(1-40%)x}$-10=$\frac{14700}{x}$ | D. | $\frac{10000}{(1-40%)x}$+10=$\frac{14700}{x}$ |
10.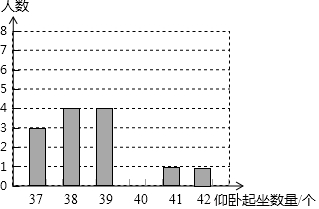 某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
(1)m=20p=15
(2)补全上面的条形统计图;
(3)被抽取的女生“仰卧起坐”测试成绩的众数是40;
(4)若该年级有320名女生,请你估计该年级女生中“仰卧起坐”测试成绩为37的人数.
 某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题| 测试成绩(个) | 学生数(名) | 百分比 |
| 37 | 3 | P% |
| 38 | 4 | 20% |
| 39 | 4 | 20% |
| 40 | N | 35% |
| 41 | 1 | 5% |
| 42 | 1 | 5% |
(2)补全上面的条形统计图;
(3)被抽取的女生“仰卧起坐”测试成绩的众数是40;
(4)若该年级有320名女生,请你估计该年级女生中“仰卧起坐”测试成绩为37的人数.
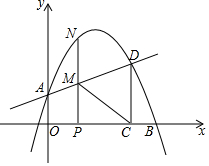 如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,$\frac{5}{2}$),过点D作DC⊥x轴,垂足为C.
如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,$\frac{5}{2}$),过点D作DC⊥x轴,垂足为C.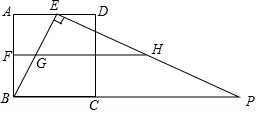 如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.
如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.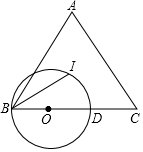 如图,△ABC中,AC=BC,I为△ABC的内心,⊙O经过B,I两点,且O在BC边上,⊙O与BC交于点D.
如图,△ABC中,AC=BC,I为△ABC的内心,⊙O经过B,I两点,且O在BC边上,⊙O与BC交于点D.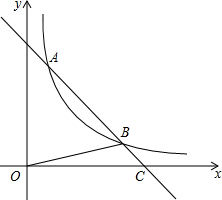 如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.
如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.