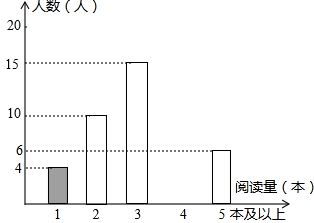
题目内容
6.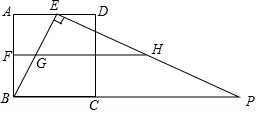 如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.
如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.(1)求BP的长;
(2)△EBM与△EPN相似吗?说明理由;
(3)求旋转角α的大小.(只耍求出α的某一个三角函数值即可)
分析 (1)只要证明△ABE∽△EPB,推出$\frac{BE}{PB}$=$\frac{AE}{BE}$,即可解决问题;
(2)结论:△EBM∽△EPN.设BN交PE于O,由FH∥BP,推出∠EHF=∠EPB=∠ENO,由∠EON=∠BOP,推出△EON∽△BOP,推出$\frac{EO}{OB}$=$\frac{ON}{OP}$,即$\frac{EO}{ON}$=$\frac{OB}{OP}$,即可推出△EOB∽△NOP,推出∠EBM=∠EPN,再证明∠BEM=∠PEN,即可解决问题;
(3)∠OEN是旋转角,∠OEN=∠OBP,可知cos∠OEN=cos∠PBN=$\frac{BN}{PB}$,由此想办法求出BN即可;
解答 解:(1)∵四边形ABCD是正方形,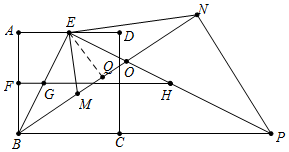
∴AB=BC=CD=AD=4,∠A=∠ABC=90°,
∵∠BEP=90°,
∴∠ABE+∠AEB=90°,∴∠EBP+∠ABE=90°,
∴∠AEB=∠PBE,∵∠A=∠BEP=90°,
∴△ABE∽△EPB,
∴$\frac{BE}{PB}$=$\frac{AE}{BE}$,
∴$\frac{2\sqrt{5}}{PB}$=$\frac{2}{2\sqrt{5}}$,
∴PB=10.
(2)结论:△EBM∽△EPN.
理由:设BN交PE于O,
∵FH∥BP,
∴∠EHF=∠EPB=∠ENO,∵∠EON=∠BOP,
∴△EON∽△BOP,
∴$\frac{EO}{OB}$=$\frac{ON}{OP}$,
∴$\frac{EO}{ON}$=$\frac{OB}{OP}$,∵∠EOB=∠PON,
∴△EOB∽△NOP,
∴∠EBM=∠EPN,
∵∠BEP=∠MEN=90°,
∴∠BEM=∠PEN,
∴△EBN∽△EPN.
(3)作EQ⊥NM于Q,
∵AF=BF,FH∥BC∥AD,
∴EG=BG=$\sqrt{5}$,
∵△EGH∽△AEB,
∴$\frac{EG}{EH}$=$\frac{AE}{AB}$=$\frac{1}{2}$,
∴EH=2EG=2$\sqrt{5}$,
∴EM=EG=$\sqrt{5}$EN=EH=2$\sqrt{5}$,
∴MN=$\sqrt{(\sqrt{5})^{2}+(2\sqrt{5})^{2}}$=5,
∵$\frac{1}{2}$•EM•EN=$\frac{1}{2}$•MN•EQ,
∴EQ=2,
∴EA=EQ,∵BE=BE,
∴△ABE≌△QBE,
∴AB=BQ=4,
∵NQ=$\sqrt{E{N}^{2}-E{Q}^{2}}$=4,
∴BN=BQ+NQ=8,
∵∠OEN是旋转角,∠OEN=∠OBP,
∴cos∠OEN=cos∠PBN=$\frac{BN}{PB}$=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题考查相似三角形综合题、正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是正确寻找相似三角形解决问题,学会添加常用辅助线,求出EQ的长是关键,属于中考压轴题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
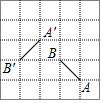 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
表一:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本校的300名学生进行投票,A,B,C三位候选人的得票数依次为105,120,75(没有弃权票,每名学生只能推荐一个),若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
 如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数. 如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离.
如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离.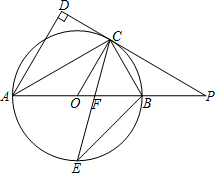 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. 某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.