题目内容
13.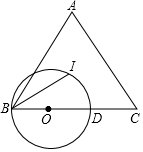 如图,△ABC中,AC=BC,I为△ABC的内心,⊙O经过B,I两点,且O在BC边上,⊙O与BC交于点D.
如图,△ABC中,AC=BC,I为△ABC的内心,⊙O经过B,I两点,且O在BC边上,⊙O与BC交于点D.(1)求证:CI为⊙O的切线;
(2)若tan∠CBI=$\frac{1}{3}$,AB=6,求BC的长.
分析 (1)连接AI延长AI交BC于H,连接OI、IC.想办法证明∠ICO+∠ICO=90°即可;
(2)由tan∠CBI=$\frac{1}{3}$,设IH=a,OB=OI=R,则BH=3a,在Rt△IOH中,R2=(3a-R)2+a2,解得R=$\frac{5}{3}$a,推出OH=BH-OB=$\frac{4}{3}$a,由OI∥AB,推出$\frac{OI}{AB}$=$\frac{OH}{BH}$=$\frac{\frac{4}{3}a}{3a}$=$\frac{4}{9}$,推出OI=$\frac{8}{3}$,a=$\frac{8}{5}$,延长即可解决问题;
解答 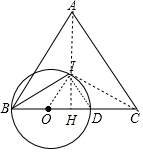 (1)证明:连接AI延长AI交BC于H,连接OI、IC.
(1)证明:连接AI延长AI交BC于H,连接OI、IC.
∵I是内心,
∴∠IAC+∠ICB+∠IBC=90°,
∵AB=AC,IA平分∠BAC,
∴AH⊥BC,∠ABC=∠ACB,∠IBC=∠ICB,
∴∠ICA+2∠ICH=90°,
∵OB=OI,
∴∠OBI=∠OIB,
∴∠IOC=2∠ICO,
∴∠ICO+∠ICO=90°,
∴∠OIC=90°,
∴IC是⊙O的切线.
(2)∵tan∠CBI=$\frac{1}{3}$,
设IH=a,OB=OI=R,则BH=3a,
在Rt△IOH中,R2=(3a-R)2+a2,
解得R=$\frac{5}{3}$a,
∴OH=BH-OB=$\frac{4}{3}$a,
∵OI∥AB,
∴$\frac{OI}{AB}$=$\frac{OH}{BH}$=$\frac{\frac{4}{3}a}{3a}$=$\frac{4}{9}$,
∴OI=$\frac{8}{3}$,a=$\frac{8}{5}$
∴BC=2BH=6a=$\frac{48}{5}$.
点评 本题考查三角形的内心与内切圆、等腰三角形的性质、切线的判定、勾股定理,平行线的性质等知识,解题的关键是学会添加常用辅助线,熟练应用内心的性质解决问题,学会利用参数解决问题,属于中考常考题型.

| A. | $\frac{x-1}{x+1}$ | B. | $\frac{x+1}{x-1}$ | C. | $\frac{x+1}{x}$ | D. | $\frac{x-1}{x}$ |
表一:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本校的300名学生进行投票,A,B,C三位候选人的得票数依次为105,120,75(没有弃权票,每名学生只能推荐一个),若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
 如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离.
如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离. 如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.
如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$. 如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系?
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系?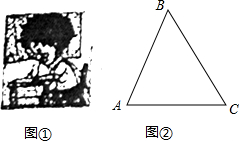 推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)