题目内容
10.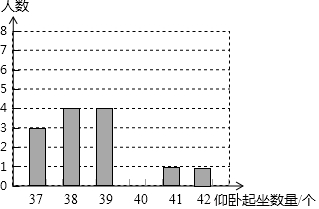 某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题| 测试成绩(个) | 学生数(名) | 百分比 |
| 37 | 3 | P% |
| 38 | 4 | 20% |
| 39 | 4 | 20% |
| 40 | N | 35% |
| 41 | 1 | 5% |
| 42 | 1 | 5% |
(2)补全上面的条形统计图;
(3)被抽取的女生“仰卧起坐”测试成绩的众数是40;
(4)若该年级有320名女生,请你估计该年级女生中“仰卧起坐”测试成绩为37的人数.
分析 (1)根据统计图中数据可以求得m的值,进而求得p的值;
(2)根据(1)中m的值,可以求得N的值,从而可以将条形统计图补充完整;
(3)根据(2)中条形统计图可以得到这组数据的众数;
(4)根据统计图中数据可以估计该年级女生中“仰卧起坐”测试成绩为37的人数.
解答  解:(1)由题意可得,
解:(1)由题意可得,
m=4÷20%=20,p%=$\frac{3}{20}×100%=15%$,
故答案为:20,15;
(2)N=20×35%=7,
补全的条形统计图,如右图所示;
(3)由(2)中的统计图可知,
被抽取的女生“仰卧起坐”测试成绩的众数是40,
故答案为:40;
(4)由题意可得,
该年级女生中“仰卧起坐”测试成绩为37的人数是:320×$\frac{3}{20}$=48,
即该年级女生中“仰卧起坐”测试成绩为37的有48人.
点评 本题考查条形统计图、用样本估计总体、统计表、众数,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
18.A,B,C三名学生竞选校学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行统计,如表一和图一:
表一:

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本校的300名学生进行投票,A,B,C三位候选人的得票数依次为105,120,75(没有弃权票,每名学生只能推荐一个),若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
表一:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本校的300名学生进行投票,A,B,C三位候选人的得票数依次为105,120,75(没有弃权票,每名学生只能推荐一个),若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
 如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离.
如图,在A港有甲、乙两艘渔船,甲船沿北偏东60°的方向以6海里/时的速度前进、乙船沿南偏东30°的方向以8海里/时的速度前进,2小时后分别到达B、C两岛,求B、C两岛的距离. 如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系?
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点,有一点P在C,D之间运动(不与C,D两点重合),在它运动过程中,试分析∠1、∠2、∠3三者之间的关系? 某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.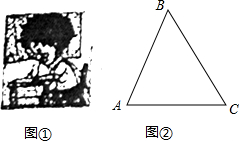 推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
推开心灵之窗,世界就在你眼前,保护视力要求人写在时眼睛和笔端的距离应超过30km,图①是一位同学的坐姿,把他的眼睛B,肘关节C和笔端的位置关系抽象成图②的△ABC,已知BC=30km,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)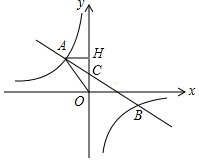 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).