题目内容
10.计算:$\frac{b}{{a}^{2}-9}•\frac{a+3}{{b}^{2}-b}$.分析 先将分母因式分解,约分后根据法则相乘即可.
解答 解:原式=$\frac{b}{(a+3)(a-3)}$•$\frac{a+3}{b(b-1)}$
=$\frac{1}{(a-3)(b-1)}$.
点评 本题主要考查分式的乘除法,一般先将能因式分解的因式分解,再将除法转化为乘法后约分,最后根据法则相乘即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
 如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | $\frac{\sqrt{3}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ |
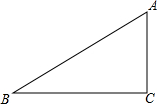 已知Rt△ABC中,AC=3,BC=4,翻折使点A和B点重合,尺规作图,画出折痕,折痕交△ABC的两边于点E、F,求EF的长度.
已知Rt△ABC中,AC=3,BC=4,翻折使点A和B点重合,尺规作图,画出折痕,折痕交△ABC的两边于点E、F,求EF的长度.