题目内容
7.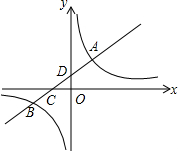 如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.
如图,一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),且与两坐标轴围成的三角形的面积为3.(1)求该一次函数的解析式;
(2)若反比例函数y2=$\frac{{k}_{2}}{x}$的图象与该一次函数的图象交于一、三象限内的A、B两点,且AC=2BC.求k2的值;
(3)在(2)的条件下,请写出当x在什么范围时,y1>y2?
分析 (1)先一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),得出OC=3,由于一次函数y=k1x+b的图象与y轴的交点是(0,b),根据三角形的面积公式可求得b的值,然后利用待定系数法即可求得函数解析式;
(2)作AE⊥x轴于点E,BF⊥x轴于点F,则AE∥BF.由△ACE∽△BCF,对应边成比例得出AE=2BF.设B点纵坐标为-n,则A点纵坐标为2n.由直线AB的解析式得出A(3n-3,2n),B(-3-$\frac{3}{2}$n,-n),再根据反比例函数y2=$\frac{{k}_{2}}{x}$的图象经过A、B两点,列出方程,解方程求出n的值,即可求得k2.
(3)求出A、B的坐标,根据图象即可求得.
解答 解:∵一次函数y1=k1x+b(k1>0)的图象经过点C(-3,0),
∴OC=3,
∵△COD的面积等于3,
∴$\frac{1}{2}$OC•OD=3,
∴$\frac{1}{2}$×3•OD=3,
解得:OD=2.
∴b=2,
∴y1=k1x+2,
把(-3,0)代入得:0=-3k1+2,解得k1=$\frac{2}{3}$,
故这个一次函数的解析式为y=$\frac{2}{3}$x+2;
(2)如图,作AE⊥x轴于点E,BF⊥x轴于点F,则AE∥BF.
∴△ACE∽△BCF,
∴$\frac{AE}{BF}$=$\frac{AC}{BC}$=2,
∴AE=2BF.
设B点纵坐标为-n,则A点纵坐标为2n.
∵直线AB的解析式为y=$\frac{2}{3}$x+2,
∴A(3n-3,2n),B(-3-$\frac{3}{2}$n,-n),
∵反比例函数y2=$\frac{{k}_{2}}{x}$的图象经过A、B两点,
∴(3n-3)•2n=(-3-$\frac{3}{2}$n)•(-n),
解得n1=2,n2=0(不合题意舍去),
∴k2=(3n-3)•2n=3×4=12.
(3)∵n=2,
∴A(3,4),B(-6,-2),
由图象可知当-6<x<0或x>3时,y1>y2.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求一次函数的解析式,三角形的面积,相似三角形的判定与性质,一次函数、反比例函数图象上点的坐标特征,难度适中.正确求出一次函数的解析式是解题的关键.

 口算能手系列答案
口算能手系列答案 如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )
如图,MN是⊙O的直径,MN=2,点A在圆周上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则△PAB周长的最小值为( )| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | $\frac{\sqrt{3}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ |
 下图中有两个变量,你能将其中一个变量看做另一个变量的函数吗?
下图中有两个变量,你能将其中一个变量看做另一个变量的函数吗?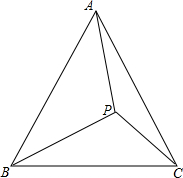 如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.
如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.