题目内容
1.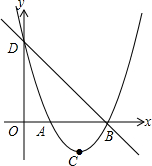 如图所示,已知二次函数y=x2-4x+m,它的图象与x轴交于A,B两点(A在B的左侧),与y轴交于点D,且满足OB=OD,顶点为C
如图所示,已知二次函数y=x2-4x+m,它的图象与x轴交于A,B两点(A在B的左侧),与y轴交于点D,且满足OB=OD,顶点为C(1)求m的值与直线BD的解析式;
(2)求抛物线顶点C的坐标;若将抛物线向左平移2个单位,再向上平移1个单位,求平移后的抛物线的解析式.
分析 (1)把点B坐标(m,0)代入y=x2-4x+m解方程即可求出m的值,再用待定系数法确定直线BD解析式.
(2)求出平移后的抛物线顶点坐标即可解决问题.
解答 解:(1)由题意,将点B坐标(m,0)代入y=x2-4x+m,
得m2-4m+m=0,即m2-3m=0,
∵m≠0,
∴m=3,
∴点D坐标(0,3),点B坐标(3,0),
设直线BD为y=kx+b,
则$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BD解析式为y=-x+3.
(2)∵抛物线解析式为y=x2-4x+3=(x-2)2-1,
∴顶点C坐标(2,-1),
平移后抛物线顶点坐标为(0,0),
∴平移后抛物线的解析式为y=x2.
点评 本题考查抛物线与x轴交点问题,二次函数图象与几何变换,灵活应用待定系数法是解决问题的关键,记住抛物线平移a的值不变,属于中考常考题型.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
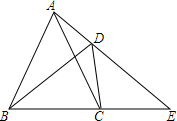 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:AC•DE=BD•CE.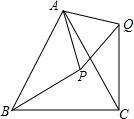 如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ. 如图,AB是⊙O的直径,D是$\widehat{BC}$的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
如图,AB是⊙O的直径,D是$\widehat{BC}$的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC并延长与DM相交于点G.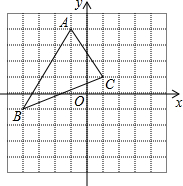 如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)
如图所示,点P(x0,y0)是△ABC内任意一点,经过平移后所得点P(x0,y0)的对应点为P1(x0+3,y0-2)