题目内容
16.计算中若出现$\sqrt{8}$、$\sqrt{\frac{5}{2}}$等这样的数时,要对它们进行化简,使被开方数不含开得尽的因数和分母.即$\sqrt{8}$=2$\sqrt{2}$,$\sqrt{\frac{5}{2}}$=$\frac{\sqrt{10}}{2}$.
实际上,在解决问题时还经常会出现$\frac{5}{\sqrt{2}}$、$\frac{3}{\sqrt{5}+\sqrt{2}}$等这样的数(即分母中含有根号),如果对它们进行化简,可简化计算,我们可这样化简:$\frac{5}{\sqrt{2}}$=$\frac{5×\sqrt{2}}{\sqrt{2}×\sqrt{2}}$=$\frac{5\sqrt{2}}{2}$.
$\frac{3}{\sqrt{5}+\sqrt{2}}$=$\frac{3(\sqrt{5}-\sqrt{2})}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}$=$\sqrt{5}$-$\sqrt{2}$,(即分母符合平方差公式即可)
①类比此方法试一试:$\frac{6}{\sqrt{3}}$=2$\sqrt{3}$,$\frac{2}{\sqrt{2}-1}$=2$\sqrt{2}$+2
②计算$\frac{\sqrt{3}+1}{\sqrt{3}-1}$-(3$\sqrt{2}-2\sqrt{3}$)(3$\sqrt{2}$+2$\sqrt{3}$)
分析 利用二次根式的乘法、除法法则即可化简.
①分别分母有理化即可.
②根据分母有理化法则以及平方差公式化简即可.
解答 解:$\sqrt{8}$=$\sqrt{2×4}$=$\sqrt{4}$×$\sqrt{2}$=2$\sqrt{2}$,$\sqrt{\frac{5}{2}}$=$\sqrt{\frac{10}{4}}$=$\frac{\sqrt{10}}{\sqrt{4}}$=$\frac{\sqrt{10}}{2}$,
故答案为2$\sqrt{2}$,$\frac{\sqrt{10}}{2}$.
①$\frac{6}{\sqrt{3}}$=$\frac{6\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{6\sqrt{3}}{3}$=2$\sqrt{3}$,$\frac{2}{\sqrt{2}-1}$=$\frac{2(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}$=2$\sqrt{2}$+2.
故答案为2$\sqrt{3}$,2$\sqrt{2}$+2.
②原式=$\frac{(\sqrt{3}+1)^{2}}{(\sqrt{3}-1)(\sqrt{3}+1)}$-[(3$\sqrt{2}$)2-(2$\sqrt{3}$)2]=$\frac{4+2\sqrt{3}}{2}$-6=2+$\sqrt{3}$-6=$\sqrt{3}$-4.
点评 本题考查二次根式的化简,解题的关键是学会分母有理化、利用平方差公式化简,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
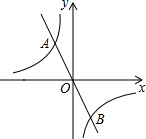 如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点
如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点
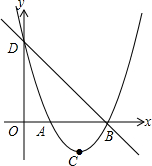 如图所示,已知二次函数y=x2-4x+m,它的图象与x轴交于A,B两点(A在B的左侧),与y轴交于点D,且满足OB=OD,顶点为C
如图所示,已知二次函数y=x2-4x+m,它的图象与x轴交于A,B两点(A在B的左侧),与y轴交于点D,且满足OB=OD,顶点为C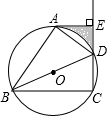 如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.
如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE. 如图所示,AB∥CD,直线MN分别交AB、CD于E、F,EG平分∠BEF,FG平分∠EFD,EG⊥FG吗?为什么?
如图所示,AB∥CD,直线MN分别交AB、CD于E、F,EG平分∠BEF,FG平分∠EFD,EG⊥FG吗?为什么?