题目内容
如图,已知线段a,c,∠α.
求作△ABC,使BC=a,AB=c,∠ABC=∠α.
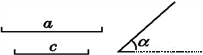
见解析
【解析】【试题分析】利用“SAS”原理作图.
【试题解析】
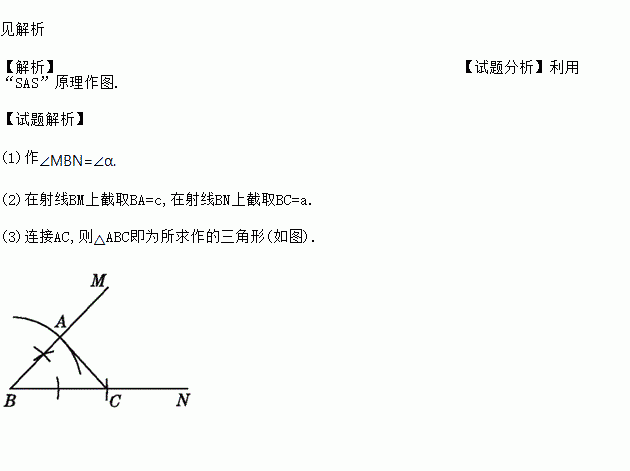
(1)作∠MBN=∠α.
(2)在射线BM上截取BA=c,在射线BN上截取BC=a.
(3)连接AC,则△ABC即为所求作的三角形(如图).
如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON=90°，OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为_____．
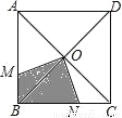
【解析】试题分析：∵四边形ABCD为正方形，点O是对角线的交点，
∴∠MBO=∠NCO=45°，OB=OC，∠BOC=90°，
∵∠MON=90°，
∴∠MOB+∠BON=90°，∠BON+∠NOC=90°，
∴∠MOB=∠NOC．
在△MOB和△NOC中，有，
∴△MOB≌△NOC（ASA）．
同理可得：△AOM≌△BON．
∴S阴影=S△BOC=... 若一个三角形的两边长分别为3和7，则第三边长可能是( )
A. 6 B. 3
C. 2 D. 11
A
【解析】试题解析：设第三条边长为x，根据三角形三边关系得：
7-3＜x＜7+3，
即4＜x＜10.
结合各选项数值可知，第三边长可能是6.
故选A. 不等式的解集在数轴上表示如图所示，则该不等式可能是___________________.
不唯一，如x－1≤0
【解析】由图形可知，不等式的解集为x≤1.只要所写的不等式的解集为x≤1，即可，答案不唯一. 用不等式表示图中的解集，其中正确的是( )
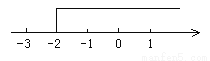
A. x≥－2 B. x＞－2 C. x＜－2 D. x≤－2
A
【解析】
试题分析：根据不等式的解集在数轴上表示出来的方法即可得到结果.
用不等式表示图中的解集为x≥－2，故选A. 根据下列已知条件,能唯一画出△ABC的是( )
A. ∠A=36°,∠B=45°,AB=4 B. AB=4,BC=3,∠A=30°
C. AB=3,BC=4,CA=1 D. ∠C=90°,AB=6
A
【解析】A. ∠A=36°,∠B=45°,AB=4,利用原理“ASA”可以画出唯一的三角形；B、C、D都不能唯一的作出三角形.故选A. 探究题：
（1）三条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（2）四条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（3）依次类推，n条直线相交，最少有__________个交点，最多有__________个交点，对顶角有__________对，邻补角有__________对.
(1)1，3；(2)1，6；(3)1， ，n(n-1)，2n(n-1)
【解析】（1）三条直线相交,最少有1个交点,最多有3个交点,如图：
（2）四条直线相交,最少有1个交点,最多有6个交点,如图:
（3）n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:（1）1,3,（2）1,6,（3）1, , ,． 如图，直线AB和CD相交于点O，则∠AOC的对顶角是__________.
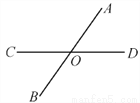
∠BOD
【解析】因为AB和CD交于点O,则∠AOC的对顶角是∠BOC,故答案为:∠BOC. 一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅匀后从中摸出一个球,请求出不是白球的概率;
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为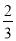
,应添加几个红球?
(1)不同意，理由见解析；（2）；（3）3.
【解析】试题分析：（1）求出分别摸到白球与摸到红球的概率，比较这两个概率，即可知道谁的可能性大，概率大则可能性就大；
（2）由（1）即可得出结论；
（3）此题考查了借助方程思想求概率的问题，解题的关键是找到等量关系．
试题解析：【解析】
（1）不同意，因为两种球数量不同，装有2个白球和1个红球，摸出白球的概率为，摸出红球的概率...