题目内容
下列平移作图错误的是( ).
A. 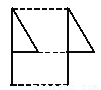 B.
B. 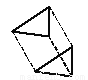 C.
C.  D.
D. 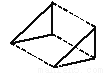
 C
【解析】试题分析:A、B、D符合平移变换,C是轴对称变换.
故选C.
C
【解析】试题分析:A、B、D符合平移变换,C是轴对称变换.
故选C.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若一个三角形的两边长分别为3和7,则第三边长可能是( )
A. 6 B. 3
C. 2 D. 11
 A
【解析】试题解析:设第三条边长为x,根据三角形三边关系得:
7-3<x<7+3,
即4<x<10.
结合各选项数值可知,第三边长可能是6.
故选A.
A
【解析】试题解析:设第三条边长为x,根据三角形三边关系得:
7-3<x<7+3,
即4<x<10.
结合各选项数值可知,第三边长可能是6.
故选A. 探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
 (1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
【解析】(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:(1)1,3,(2)1,6,(3)1, , ,.
(1)1,3;(2)1,6;(3)1, ,n(n-1),2n(n-1)
【解析】(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有对,邻补角有对.
故答案为:(1)1,3,(2)1,6,(3)1, , ,. 如图,直线AB和CD相交于点O,则∠AOC的对顶角是__________.
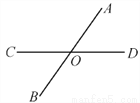
 ∠BOD
【解析】因为AB和CD交于点O,则∠AOC的对顶角是∠BOC,故答案为:∠BOC.
∠BOD
【解析】因为AB和CD交于点O,则∠AOC的对顶角是∠BOC,故答案为:∠BOC. 如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
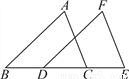
 (1) 9厘米;(2) 140°;(3) AB=FD、AC=FE、BC=DE、BD=CE;(4) AB∥FD、AC∥FE.
【解析】试题分析:(1)根据平移的性质可得CE=3cm,然后根据BE=BC+CE即可得出结论;
(2)根据平移的性质得出∠FDE的度数,然后根据邻补角互补即可得出答案;
(3)直接根据平移的性质即可得出结论;
(4)根据平移的性质即可得出结论.
...
(1) 9厘米;(2) 140°;(3) AB=FD、AC=FE、BC=DE、BD=CE;(4) AB∥FD、AC∥FE.
【解析】试题分析:(1)根据平移的性质可得CE=3cm,然后根据BE=BC+CE即可得出结论;
(2)根据平移的性质得出∠FDE的度数,然后根据邻补角互补即可得出答案;
(3)直接根据平移的性质即可得出结论;
(4)根据平移的性质即可得出结论.
... 用计算器求下列格式的值(结果精确到0.0001).
(1)tan63°27′;
(2)cos18°59′27″;
(3)sin67°38′24″.
 (1)2.0013;(2)0.9456;(3)0.9248.
【解析】试题分析:将度、分、秒统一为度,然后利用计算器即可求出结果.
试题解析:
【解析】
(1)tan63°27′=tan63.45°≈2.0013;
(2)cos18°59′27″=cos18.9908°≈0.9456;
(3)sin67°38′24″=sin67.64°≈0.9248.
(1)2.0013;(2)0.9456;(3)0.9248.
【解析】试题分析:将度、分、秒统一为度,然后利用计算器即可求出结果.
试题解析:
【解析】
(1)tan63°27′=tan63.45°≈2.0013;
(2)cos18°59′27″=cos18.9908°≈0.9456;
(3)sin67°38′24″=sin67.64°≈0.9248. 用计算器求tan35°的值,按键顺序是 .
 MODE,tan,35,=.
【解析】
试题分析:本题要求同学们能熟练应用计算器,会用科学记算器进行计算.
试题解析:根据已知一个角的正弦值求这个角的算法:先按MODE,选择模式;再键tan,35,最后按=;得到这个角的函数值.
MODE,tan,35,=.
【解析】
试题分析:本题要求同学们能熟练应用计算器,会用科学记算器进行计算.
试题解析:根据已知一个角的正弦值求这个角的算法:先按MODE,选择模式;再键tan,35,最后按=;得到这个角的函数值. 一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅匀后从中摸出一个球,请求出不是白球的概率;
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为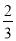 ,应添加几个红球?
,应添加几个红球?
 (1)不同意,理由见解析;(2);(3)3.
【解析】试题分析:(1)求出分别摸到白球与摸到红球的概率,比较这两个概率,即可知道谁的可能性大,概率大则可能性就大;
(2)由(1)即可得出结论;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系.
试题解析:【解析】
(1)不同意,因为两种球数量不同,装有2个白球和1个红球,摸出白球的概率为,摸出红球的概率...
(1)不同意,理由见解析;(2);(3)3.
【解析】试题分析:(1)求出分别摸到白球与摸到红球的概率,比较这两个概率,即可知道谁的可能性大,概率大则可能性就大;
(2)由(1)即可得出结论;
(3)此题考查了借助方程思想求概率的问题,解题的关键是找到等量关系.
试题解析:【解析】
(1)不同意,因为两种球数量不同,装有2个白球和1个红球,摸出白球的概率为,摸出红球的概率... 若ax>b,ac2<0,则x________.
 <
【解析】由ac2<0,结合c2为正可知a<0,
对ax>b两边同时除以a,得x< .故答案为:<.
<
【解析】由ac2<0,结合c2为正可知a<0,
对ax>b两边同时除以a,得x< .故答案为:<. 
