题目内容
1．
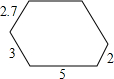如图，一个六边形的每个内角都是120°，连续四边的长依次是2.7、3、5、2，则该六边形的周长是20.7．
分析 先延长并反向延长AB，CD，EF，构成一个等边三角形，再将这个六边形以外的多边形减去即可得这个六边形的周长．
解答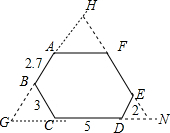 
解：如图，延长并反向延长AB，CD，EF．
∵六边形ABCDEF的每个内角都是120°
∴∠G=∠H=∠N=60°，
∴△GHN是等边三角形，
∴六边形ABCDEF的周长=HN+AG+CD=（3+5+2）+（2.7+3）+5=20.7．
答：该六边形周长是20.7．
故答案为：20.7．
点评 本题考查了多边形的内角和外角，等边三角形的判定与性质，解决本题的关键是构造等边三角形，根据等边三角形的三边相等的性质求解．
练习册系列答案
同步奥数系列答案
相关题目
5．
老北京的老行当中有一行叫做“抓彩卖糖”：商贩将高丽纸裁成许多小条，用矾水在上面写上糖的块数，最少一块，多的是三块或五块，再将枝条混合在一起．游戏时叫儿童随意抽取一张，然后放入水罐中浸湿，即出现白道儿，按照上面的白道儿数给糖．一个商贩准备了10张质地均匀的纸条，其中能得到一块糖的纸条有5张，能得到三块塘的纸条有3张，能得到五块糖的纸条有2张．从中随机抽取一张纸条，恰好是能得到三块塘的纸条的概率是（ ）
老北京的老行当中有一行叫做“抓彩卖糖”：商贩将高丽纸裁成许多小条，用矾水在上面写上糖的块数，最少一块，多的是三块或五块，再将枝条混合在一起．游戏时叫儿童随意抽取一张，然后放入水罐中浸湿，即出现白道儿，按照上面的白道儿数给糖．一个商贩准备了10张质地均匀的纸条，其中能得到一块糖的纸条有5张，能得到三块塘的纸条有3张，能得到五块糖的纸条有2张．从中随机抽取一张纸条，恰好是能得到三块塘的纸条的概率是（ ）| A． | $\frac{1}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{2}$ |
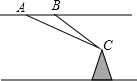如图，飞机的飞行高度为2500米，在A点处测得某电视塔尖点C的俯角为30°，保持方向不变前进1200米到达B点时测得该电视塔尖点C的俯角为45°．请计算电视塔的高度（结果保留整数，$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
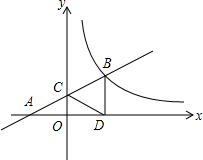如图，在直角坐标系xOy中，直线y=mx+1经过点A（-2，0）与y轴正半轴交于C点，与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点B，过B作BD⊥x轴于D，连接DC，若AC=CB．
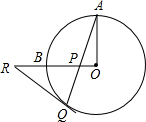如图，OA、OB是⊙O的两条互相垂直的半径，P为OB上任一点，AP的延长线交⊙O于点Q，过点Q作⊙O的切线交OB的延长线于点R，求证：RP=RQ．
如图，抛物线y=ax2+bx+c与y轴交于A点，过点A的直线y=$\frac{1}{2}$x+1与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0），又抛物线的对称轴为x=$\frac{17}{10}$．